Chapter 3

WHY DOESN'T ANYONE EVER GET YOUNGER?

The Last Question

In Isaac Asimov's 1956 short story "The Last Question," a slightly drunk man by the name of Alexander Adell gets seriously worried about the energy supply of the universe. He reasons that, while energy itself is conserved, the useful fraction of energy will inevitably run out. Physicists call this useful energy, which can bring about change, free energy. Free energy is the counterweight of entropy. As entropy in-creases, free energy decreases, and change becomes impossible.

In Asimov's story, tipsy Adell hopes to overcome the second law of thermodynamics, which has it that entropy cannot decrease. He approaches a powerful automatic computer, called Multivac, and asks: “How can the net amount of entropy of the universe be massively decreased?" After a pause, Multivac responds: "INSUFFICIENTDATA FOR MEANINGFUL ANSWER."

Adell's worry - the second law of thermodynamics - is familiar to all of us, even if we don't always recognize it for what it is. It's one of the first lessons we learn as infants: things break, and some things that break can't be fixed. It isn't just Mommy's favorite mug that ultimately suffers this fate. Eventually, everything will be broken and unfixable: your car, you, the entire universe,

It seems our experience that things irreversibly break is at odds with what we discussed in the previous chapter, that the fundamental laws of nature are time-reversible. And in this case, we can't just chalk this mismatch up to our fallible human senses, because we observe irreversibility in many systems much simpler than brains.

Stars, for example, form from hydrogen clouds, fuse hydrogen to heavier atomic nuclei, and emit the resulting energy in the form of particles (mostly photons and neutrinos). When a star has nothing left to fuse, it dims or, in some cases, blasts apart into a supernova. But we have never seen the reverse. We have never observed a dim star that took in photons and neutrinos and then split heavy nuclei into hydrogen before spreading out to become a hydrogen cloud. The same goes for countless other processes in nature: Coal burns. Iron rusts. Uranium decays. But we never see the reverse processes.

Superficially, this looks like a contradiction. How can time-reversible laws possibly give rise to the evident time-irreversibility we observe? To understand how this can be, it helps to sharpen the problem. All the processes I just described are time-reversible in the sense that we can mathematically run the evolution law backward in time and recover the initial state. That is to say, the problem is not that we cannot run the movie backward; the problem is that when we run the movie backward, we immediately see that something isn't right: shards of glass jump top and fill a window frame, car tires pick up rubber streaks from the street, water drops lift from an umbrella and rise into the sky. Math may allow that, but it clearly isn't what we observe.

This mismatch between our theoretical and intuitive expectations comes from forgetting about the second ingredient we need to ex-plain observations. Besides the evolution law, we need an initial condition. And not all initial conditions are created equal.

Suppose you want to prepare the batter to bake a cake. You put flour into a bowl, add sugar, a pinch of salt, and maybe some vanilla extract. Then you put butter on top, break a few eggs, and pour income milk. You begin mixing the ingredients, and they quickly turn Into a smooth, featureless substance. Once that has happened, the batter won't change anymore. If you keep on mixing, you will still move molecules from one side of the bowl to the other, but on average the batter remains the same. Everything is as mixed up as it can be, and that's it. Basically, our universe will end up like this too: as mixed-up as it can be, with no more change, on average.

In physics, we call a state that doesn't change on average like the fully mixed batter-an equilibrium state. Equilibrium states have reached maximum entropy; they have no free energy left. Why does the batter come into equilibrium? Because it's likely to happen. If you turn on the mixer, it's likely to mash the eggs into the flour but very unlikely to separate the two. This would also happen without the mixer, because the molecules in the ingredients don't sit entirely still, but it would take much longer." The mixer acts like a fast-forward button.

It's the same for the other examples: they are likely to happen only in one direction of time. When pieces of a broken window fall to the ground, their momentum disperses in tiny ripples in the ground and shock waves in the air, but it is incredibly unlikely that ripples in the ground and the air would ever synchronize in just the right way to catapult the broken glass back into the right position. Sure, it's possible mathematically, but in practice it's so unlikely, we never see it happening.

['In theory. In practice, the eggs would rot long beefcake that, so please don't try it at home]

The equilibrium state is the state you are likely to reach, and the state you are likely to reach is the state of highest entropy-that's just how entropy is defined. The second law of thermodynamics, hence, is almost tautological. It merely says that a system is most likely to do the most likely thing, which is to increase its entropy. It is only almas tautological because we can calculate the relation between entropy and other measurable quantities (say, pressure or density), making relaxation to equilibrium quantifiable and predictive.

It sounds rather unremarkable that likely things are likely to happen. Pots break irreversibly because they're unlikely to unbreak. Douthat’s not exactly a deep revelation. But if you pursue this thought further, it reveals a big problem. A system can evolve toward a more likely state only if the earlier state was less likely. In other words, you have to start from a state that's not in equilibrium to begin with. The only reason you can prepare a batter is that you have eggs and butter and flour, and those are not already in equilibrium with one another. The only reasons you can operate a mixer is that you are not in equilibrium with the air in your room" and our Sun is not in equilibrium with interstellar space. The entropy in all these systems isn’t remotely as large as it could be. In other words, the universe isn't in equilibrium.

Why is that? We don't know, but we have a name for it: the pathopoeias. The past-hypothesis says that the universe started out in a state of low entropy - a state that was very unlikely and that entropy has gone up ever since. It will continue to increase until the universe has reached the most likely state, in which nothing more will change, on average.

["Assuming the tar Templemore is above or below body temperature, because then you'd be dead if you were in equilibrium with it. If it happens to be at body temperature, I applaud your enduring.]

For now, entropy can remain small in some parts of the universe like in your fridge or, indeed, on our planet as a whole provided these low entropy parts are fed with free energy from elsewhere. Our planet currently gets most of its free energy from the Sun, some of it from the decay of radioactive materials, and a little from plain old gravity. We exploit this free energy to bring about change: we learn, we grow, we explore, we build and repair. Maybe at some point in the future we will succeed with creating energy from nuclear fusion ourselves, which will expand our capacity to bring about change. That way, if we smartly use the available free energy, we might manage to keep entropy low and our civilization alive for some billion years. But free energy will run out eventually.

This is why the universe has a direction forward in time, the arrow of time it's the direction of entropy increase; it points one way and not the other. This entropy increase is not a property of the evolution laws. The evolution laws are time-reversible. It's just that intone direction the evolution law brings us from an unlikely to a likely state, and that transition is likely to happen. In the other direction, the law goes from a likely to an unlikely state-and that (almost]never happens.

So why doesn't anyone ever get younger? The biological processes involved in aging and exactly what causes them are still the subject of research, but loosely speaking, we age because our bodies accumulate errors that are likely to happen but unlikely to spontaneously reverse. Cell repair mechanisms can't correct these errors indefinitely and with perfect fidelity. Thus, slowly, bit by bit, our organs function a little less efficiently, our skin becomes a little less elastic, our wounds heal a little more slowly. We might develop a chronic illness, dementia, or cancer. And eventually something breaks that can't be fixed. Avital organ gives up, a virus beats our weakened immune system, or a blood clot interrupts oxygen supply to the brain. You can find many different diagnoses in death certificates, but they're just details. What really kills us is entropy increase.

So far, I have just summarized the currently most widely accepted explanation for the arrow of time, which is that it's a consequence of entropy increase and the past-hypothesis. Now let us talk about how much of this we actually know and how much is speculation. The past hypothesis that the initial state of the universe had low Entropy is a necessary assumption for our theories to describe what we observe. It's a good explanation so far as it goes, but we don't currently have a better explanation than just postulating it. The question why an initial state was what it was just isn't answerable with the theories we currently have. The initial state must have been something, but we can't explain the initial state itself; we can only examine whether a specific initial state has explanatory power and gives rise to predictions that agree with observations. The past-hypothesis is a good hypothesis in the sense that it explains what we see. However, to explain the initial state by something else than a yet earlier initial state, we would need a different type of theory.

Of course, physicists have put forward such different theories. In Roger Penrose's conformal cyclic cosmology, for example, the entropy of the universe is actually destroyed at the end of each eon, so the next con starts afresh in a low-entropy state. This does indeed explain the past hypothesis. The price to pay is that information is lodestone for good. Sean Carroll thinks that new, low-entropy universes are created out of a larger multiverse, a process that can continue to happen indefinitely. And Julian Barbour posits that the universe started from a "Janus point" at which the direction of time changes, so actually there are two universes starting from the same moment in time. He argues that entropy isn't the right quantity to consider and that we'd be better off thinking about complexity instead.

You probably know what I am going to tell you next: these ideas are all well and fine, but they're not backed up by evidence. Feel free to believe them-I don't think any evidence speaks against them cither but keep in mind that at this point they're just speculation.

I do have a lot of sympathy for Julian Barbour's argument, however. Not so much because, according to Barbour, time changes direction [which I have no strong opinion about), but because I also don't think entropy is of much use when describing the universe as a whole. To see why, I first have to tell you about the math I swept under the rug with the vague phrase "on average."

Entropy is formally a statement about the possible configurations of a system that leave some macroscopy properties unchanged. For the batter, for example, you can ask how many ways there are to place the molecules [of sugar, flour, eggs, and so on) in a bowl so you get a smooth batter. Each such specific arrangement of the molecules is called a microstate of the system. A microstate is the full information about the configuration: for example, the position and velocity of all those single molecules.

The smooth batter, on the other hand, is what we call a macrostate. It's what I referred to earlier loosely as the average that doesn't change. A macrostate can come about by many different microstates that are similar in some specific sense. In the batter, for example, the microstates are all similar in that the ingredients are approximately equally distributed. We choose this macrostate because we can't distinguish one approximately equal distribution of molecules in the batter from any other. For us, they're all pretty much the same.

The initial state, in which the eggs are next to the butter and the sugar is on top of the flour, is also a macrostate, but it's very different from the batter-you can clearly distinguish the state before mixing from that after mixing. To get the state before mixing, you'd have to put the molecules in the right regions; egg molecules in the egg region, butter molecules in the butter region, and so on. The molecules are ordered in this initial state, whereas after mixing they aren't ordered anymore. This is why entropy increase is also often described as the destruction of order.

The mathematical definition of entropy is a number assigned to a macrostate: the number of microstates that can give rise to it. A macrostate that you can get from many microstates is likely, hence the entropy of such a macrostate is high. A macrostate that can come about from only comparably few microstates, on the other hand, is unlikely and has low entropy. The mixed batter, in which the molecules are randomly distributed, has many more microstates than the initial, unmixed batter. Thus, the mixed batter has high entropy; the unmixed one, low.

To give you a visual idea of why this is, suppose we have only two ingredients, and we don't have 102 or so molecules but only 36, half of them flour, the other half sugar. I have drawn these in a grid, and marked each flour molecule with a gray square and each sugar molecule with a white square (figure 4). Initially the two substances are cleanly separated: flour at the bottom, sugar on top (figure 4a). Now let us simulate the mixer by randomly exchanging the positions of two adjacent squares, either horizontally or vertically. I have drawn a first step so you see how this works (figure 4h).

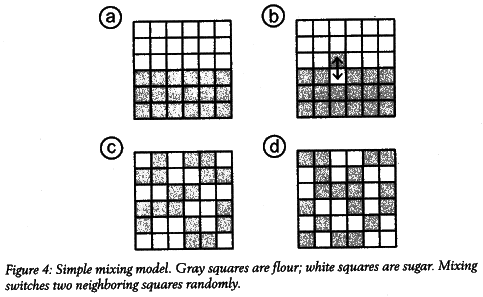
If we continue to randomly swap neighbors, the molecules will eventually be randomly distributed (figure 4c). What happens is not that the molecules stay in the same place, but they remain equally mixed up. After some more mixing they might look like they do figure 4d. That is, a large number of random swaps gives the same average distribution as if you'd randomly thrown the molecules into the bowl. So instead of having to think about exactly what the mixer does, we can instead just look at the difference between the initial and final distribution.

Let us then define a macrostate of a smooth batter as one in which the sugar and flour squares are approximately equally distributed on top and bottom, say 8 to 10 sugar molecules in the top half (as in figures 4c and 4d). The relevant point is now that there are many more microstates that belong to this macrostate than there are for the initial, cleanly separated state. Indeed, if you don't distinguish molecules of the same type, there's only the initial microstate I drew on the top left, whereas there are many final microstates that are approximately evenly distributed.

This is why entropy is larger in the approximately even distribution, and also why the two substances are unlikely to spontaneously unmix again it'd require a very specific sequence of random swaps. The sequence required for unmixing becomes less likely the more molecules you mix. Soon it becomes so unlikely that the probability for it to happen in a billion years is ridiculously tiny you never see it happening.

Now that you know how entropy is formally defined, let us have a closer look at this definition: entropy counts the number of microstates that can give rise to a certain macrostate. Notice the word can. The state of system is always in only one microstate. The statement that it "can" be in any other state is counterfactual it refers to states that do not existing reality; they exist only mathematically. We consider them just because we do not know exactly what the true state of the system is.

Entropy thus is really a measure of our ignorance, not a measure for the actual state of the system. It quantifies which differences between microstates we think aren't interesting. We don't think the specific distribution of the molecules in the batter is interesting, so we lump them together in one macrostate and declare that "high entropy."

This kind of reasoning makes a lot of sense if you want to calculate how quickly a system evolves into a particular macrostate. It therefore works well for all the purposes that the notion of entropy was invented for: steam engines, cooling cycles, batteries, atmospheric circulation, chemical reactions, and so on. We know empirically that it describes our observations of these systems just fine.

This reasoning is, however, inadequate if we want to understand what happens with the universe as a whole, and that's for three reasons. First, and in my mind most important, it's inadequate because our notion of a macrostate implicitly defines already what we meanly change. A state that has reached maximum entropy, according tour definition of a macrostate, still changes (you are still moving better from one side of the bowl to the other even when it already looks smooth). It's just that, according to our current theories, this changes irrelevant. We don't know, however, whether this will remain so with theories we may develop in the future. I have illustrated what I mean in figure 5. You can think of these as two possible microstates at the end of the universe, ten lonely particles that are randomly distributed in empty space. If the first microstate(left) changed to the second (right), you wouldn't call that much of a change. You'd average over it and lump them both together in the same macrostate.

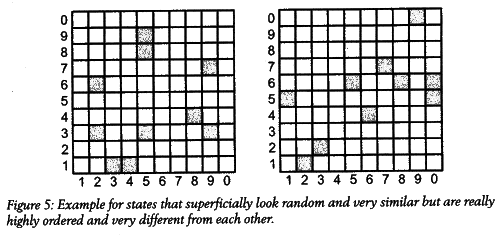
But now have a closer look at the locations of these particles on the grid. In the example on the left, they are located at (3,1), (4,1), (5,9), (2,6), (5,3), (5,8), (9,7), (9,3), (2,3), and (8,4). In the example on the right, they are at (0,5), (7,7), (2,1), (5,6), (6,4), (9,0), (1,5), (3,2), (8,6), and (0,6). The super-nerds among you will immediately have recognized these sequences as the first twenty digits of n and of y (the Euler-Mascheroni constant). The distribution of these particles might look similar to our eyes, but a being with the ability to grasp the sequence of the distribution could clearly distinguish them; they were created by two entirely different algorithms.

Of course, this example is an ad hoc construction and not applicable to our actual theories, but it illustrates a general point. When we lump together "similar' states in a macrostate, we need a notion of "similarity." We derive this notion from current theories that are based onwhat we ourselves think of as similar. But change the notion of similarity and you change the notion of entropy. To borrow the terms coined by David Bohm, the explicate order, which our current theory qualify, might one day reveal an implicate order that we have missed so far.

To me, that's the major reason the second law of thermodynamics shouldn’t be trusted for conclusions about the fate of the universe. Our notion of entropy is based on how we currently perceive the universe; I don't think it's fundamentally correct.

There are two more reasons to be skeptical of arguments about the entropy of the universe. One is that counting microstates and com-paring their numbers becomes tricky if a theory has infinitely many microstates, and that's the case for all continuous-field theories, It is possible to define entropy in those cases, but whether it's still a meaningful quantity is questionable. It's generally a bad idea to compare Infinity to infinity, because the outcome depends on just how you define the comparison, so any conclusion you draw from such an exercise becomes physically ambiguous.

Finally, we don't actually know how to define entropy for gravity or for space-time, but this entropy plays a most important role in the evolution of the universe. You might have noticed that, according tour current theories, matter in the universe starts out as an almost evenly distributed plasma. That plasma must have had low entropy according to the past hypothesis. But I told you earlier that the smooth batter had high entropy. How does this fit together?

It fits together if you take into account the fact that gravity makes the almost even, high-density plasma in the early universe extremely unlikely. Gravity wants to clump things, but for some reason they weren’t very clumped when the universe was young. That's why the initial state had low entropy. Once it evolves forward in time, sure enough, the plasma begins to clump, forming stars and galaxies because that's likely to happen. This doesn't happen in the batter, because the gravitational force isn't strong enough for such a small amount of matter at comparably low density. It's because of the different role of gravity that the batter and the early universe are two very different cases, and why the one has high entropy, the other onflow entropy.

However, to make this case quantitative, we'd have to understand how to assign entropy to gravity. While physicists have made some attempts at doing that, we still don't really know how to do It, because we don't know how to quantize gravity.

For these reasons, I personally find the second law of thermodynamics highly suspect and don't think conclusions drawn from it today will remain valid when we understand better how gravity and quantum mechanics work.

In Asimov's short story, the universe gradually cools and darkens. The last stars burn out. Life as we know it ceases to exist and is superseded by cosmic consciousnesses, disembodied minds that span galaxies and drift freely through space. Cosmic AC, the last and greatest version of the Multivac series, is again tasked with answering the question bow to decrease entropy. Yet again, it stoically replies, THERE IS AS YET INSUFFICIENT DATA FOR A MEANING.FUL ANSWER."

Eventually, the last remaining conscious beings’ fuse with the Achish now resides "in hyperspace" and is "made of something that [is]neither matter nor energy." Finally, it finishes its computation.

The consciousness of AC encompassed all of what had once been a Universe and brooded over what was now Chaos. Step by step, it must be done. And AC said, "LET THERE BE LIGHT!" And there was light.

The Problem of the Now Einstein’s greatest blunder wasn't the cosmological constant, and neither was it his conviction that God doesn't play dice. No, his greatest blunder was spending to a philosopher named Rudolf Carnap about the Now, with a capital n.

"The problem of the Now," Carnap wrote in 1963, "worried Einstein seriously. He explained that the experience of the Now means something special for man, something different from the past and the future, but that this important difference does not and cannot occur within physics."

I call it Einstein's greatest blunder because, unlike the cosmos-logical constant and his misgivings about indeterminism, this alleged problem of the Now still confuses philosophers, and some phis-cists too.

The problem is often presented like this. Most of us experience a present moment, which is a special moment in time, unlike the past and unlike the future. But if you write down the equations governing the motion of, say, some particle through space, then this particle is described, mathematically, by a function for which no moment is special. In the simplest case, the function is a curve in space-time, which just means the object changes its location with time. Which moment, then, is Now?

You could argue rightfully that as long as there's just one particle, nothing is happening, and so it's unsurprising that no indication of change appears in the mathematical description. If, in contrast, the particle could bump into some other particle, or take a sudden turn, then these instances could be identified as events in space-time. That something happens seems a minimum requirement to meaningfully talk of change and make sense of time. Alas, that still doesn't tell you whether these changes happen to the particle Now or at some other time.

Now what? Some physicists, for example Fay Dower, have argued that ac-counting for our experience of the Now requires replacing the cur-rent theory of space-time with another one. David Mermin has claimed it means a revision of quantum mechanics is due. And Lee Smolin has boldly declared that mathematics itself is the problem. Itis correct, as Smolin argues, that mathematics doesn't objectively describe a present moment, but our experience of a present moment is not objective it's subjective. And that subjectivity can well be described by mathematics.

Don't get me wrong. It seems likely to me that we will one day have to replace the current theories with better ones. But understandIng our perception of the Now alone does not require it. The present theories can account for our experience; we merely have to remember that humans are not elementary particles.

The property that allows us to experience the present moment as unlike any other moment is memory we have an imperfect memory of events in the past and we do not have a memory of events in the future. Memory requires a system of some complexity, one with muletiple states that are clearly distinguishable and stable for extended periods of time. Our brain has the required complexity. But to under-stand better what is going on, it helps to leave aside consciousness. Wean do this because memory is not exclusive to conscious systems. Many systems much simpler than human brains also have memory, Solet us have a look at one of those: mica.

Mica is a class of naturally occurring minerals, some of it as old as a billion years. Mica is soft for a mineral, and small particles passing through it maybe from radioactive decays in surrounding rocks can leave permanent tracks in it. This makes mica a natural particle detector. Indeed, particle physicists have used old samples of mica to search for traces of rare particles that might have passed through. These studies have remained inconclusive, but they're not the relevant point here. I am merely telling you this because mica, though it arguably has low levels of consciousness, clearly has memory.

Memories in mica don't fade like ours do. But, like us, mica has a memory of the past and not of the future. That means that at any particular moment, mica has information about what has happened but no information regarding what's about to happen. It would be a stretch to say that mica has experience of any kind, but it keeps track of time it knows about the Now.

From mica we can learn that if we want to describe a system with memory, just looking at the proper time as we did in the previous chapter isn't enough. For each moment of proper time, we need task, "What times does the system have a memory of?" The fact that this memory abruptly ends at the proper time Itself is why each moment is special as it happens.

If that sounds confusing, imagine your perception of time as a collection of photographs in different stages of fading. The moment you call Now is the photograph that's least faded. The more faded a photograph is, the more it is in the past. You don't have photographs of the future. At each moment, the Now is your most vivid, most re-cent photo, with a long trail of fading snapshots behind it and a blank for the future.

Of course, this is an overly simplistic description of human memory. Our actual memory is much more complicated than this. To begin with, we retain some memories and not others, we have several different types of memory for different purposes, and sometimes we believe we have memories of things that didn't happen. But these neurological subtleties aren't important here. What's important is that the present moment is special because of its prominent positioning your memory. And the next moment is special too: in each moment, your perception of that same moment stands out.

This is why our experience of a Now is perfectly compatible with the block universe in which the past, present, and future are all equally real. Each moment subjectively feels special at that very moment, but objectively that's true for every moment.

We can see, then, that the origin of the problem of the Now is noting the physics, and not in the mathematics, but in the failure to dis-tongues the subjective experience of being inside time from the timeless nature of the mathematics we use to describe it. According ocarina, Einstein spoke about "the experience of the Now [that]means something special for man." Yes, it means something special for man; it means something special for all systems that store memory. However, this does not mean, and certainly does not necessitate, that there is a present moment that is objectively special in the math-lemmatical description. Objectively, the Now doesn't exist, but subjectively we perceive each moment as special. Einstein should not homeworker.

The upshot please forgive me-is that Einstein was wrong. It is possible to describe the human experience of the present moment with the "timeless" mathematics we now use for physical laws; it isn’t even difficult. You don't have to give up the standard interpretation of quantum mechanics for it, or change general relativity, or overhaul mathematics. There is no problem of the Now.

Incidentally, Carnap answered Einstein's worry about the Now quite as I just did. Carnap remembers remarking to Einstein that "all that occurs objectively can he described in science" hut that the “peculiarities of man's experiences with respect to time, including his different attitude towards past, present, and future, can be described and (in principle) explained in psychology."

I'd have said it's explained by neurobiology and added that biology’s ultimately also based on physics. (If this upsets you, you will especially enjoy the next chapter.) Nonetheless, I agree with Carnap that it’s important to distinguish objective mathematical descriptions of a system from the subjective experience of being part of the system.

So there is no problem of the Now. But the discussion about memory is useful to illustrate the relevance of entropy increase for our perception of an arrow of time. I told you in the previous section why for-ward in time looks different from backward in time, but not why it’s the direction of entropy increase that we perceive as forward. Mica illustrates why.

The reason mica doesn't have a memory of the future is that creating its memory increases entropy. A particle goes through the mineral and kicks a neatly aligned sequence of atoms out of place. The atoms remain displaced because part of the energy that moved them dis-parses into thermal motion and maybe some sound waves. In that process, entropy increases. The reverse process would require fluctuations in the mineral to build up and emit a particle that heals attack in the mineral perfectly. That would decrease entropy and is, hence, incredibly unlikely to happen. The entire reason that we see a record in the mineral is that this process is unlikely to spontaneously reverse.

Memory formation in the human brain is considerably more differcult than that, but it, too, goes back to low-entropy states that left traces in our brain. Say you have a memory of your graduation day. Itis likely that this event was in the past and created by light that hit your retina. It is incredibly unlikely that the event will instead be in the future and somehow suck the memory out of your brain. Such things just don't happen. And the reason they don't happen is that entropy increases in only one direction of time.

In the long run, of course, further entropy increase will wash out any memory.

In summary, neither our experience of an arrow of time nor that of a present moment requires changing the theories we currently use. Of course, some physicists have nevertheless put forward proposals for different laws that are bona fide time irreversible, but such modifications are unnecessary to explain currently available observations. For all we know, the block universe is the correct description of nature.

Many people feel uneasy when they first realize that Einstein’s theories imply that the past and future are as real as the present, and that the present moment is only subjectively special. Maybe you are one of them. If so, it is worth combating your uneasiness, because the reward is seeing that our existence transcends the passage of time. We always have been, and always will be, children of the universe.

Brains. In Empty Space.

We will all come back At the end of time As a brain in a vat, floating around And purely mind - Sabir Senefelder, "Schrodinger's Cat".

The realization that reality is but a sophisticated construction our mind produces from sensory input, and that our perception of it can therefore change if the input changes, has made its way into pop culture in movies like The Matrix (in which the protagonist is raised in a computer simulation only to discover that reality looks rather differ-Ent) and Inception fin which the protagonists struggle to devise ways of telling dream from reality) and Dark City (in which memories are adjusted each midnight), though such accounts tend to shy away from suggesting that reality ultimately does not exist. There are places even Hollywood won't go.

It's not a new idea that you may be just an isolated brain in a vat, or in an empty universe, with sensory input that creates the illusion of being a human on planet Earth. The idea that we can't really know anything for sure besides the fact that we ourselves exist is an old philosophy known as solipsism. As so often, the first written record of someone contemplating this possibility comes from a Greek philosopher, Gorgias, who lived about 2,500 years ago. But solipsism is more commonly associated with Rene Descartes, who summed it up with “I think, therefore I am," adding at length that, of all the other things, he could never be quite certain.

You may have hoped that physics gets you out of this conundrum, but it doesn't. It makes it worse. That's because in my elaboration about entropy increase, I have omitted an inconvenient detail: entropy actually doesn't always increase. And if it decreases, weird things happen.

Let us look again at our simplified batter-mixing model with the36 squares. Suppose you have reached a state of high entropy, a smooth macrostate with 8 to 10 gray squares in the top half. Thing is, if you keep on randomly swapping neighbors, the state will not forever stay smooth, Every once in a while, just coincidentally, there'll be only 7sugar molecules in the upper half. Keep on swapping and you'll come across an instance when there are only 6. It's unlikely to remain so furlong, and probably you'll soon get back to a smooth state. But if you just stubbornly keep on mixing the squares, eventually you'll have only 5, 4, 3, 2, 1, and even O gray squares in the upper half. You will have gone back all the way to the initial state. Entropy, it will seem, has decreased.

This isn't a mistake; it's how entropy works. After you have maximized it and reached an equilibrium state, entropy can coincidentally decrease again. Small out-of-equilibrium fluctuations are likely; big-ger ones, less likely. A substantial decrease of entropy in the mixing of a real batter is so unlikely that you'd not have seen it happening yet even if you'd been mixing since the Big Bang. But if you could just mix long enough, eggs would eventually reassemble and butter would form a clump again. This isn't a purely mathematical speculation cither-spontaneous decreases in entropy can, and have been, observed in small systems. Tiny beads floating in water, for example, have been observed to occasionally gain energy from the random motion of the water molecules. This temporarily defies the second law of thermodynamics.

Such entropy fluctuations create the following problem. If we take together everything we know about the universe, it looks as though it’ll go on expanding for an infinite amount of time. As entropy increases, the universe becomes more and more boring. Eventually, when all the stars have died, all matter has collapsed to black holes, and those lack holes have evaporated, it ‘Il contain only thinly distributed radiation and particles that occasionally bump into one another.

But this isn't the end of the story, because infinity is a really longtime. In an infinite amount of time, anything that can happen will eventually happen no matter how unlikely.

This means that in that boring, high-entropy universe, there'll be regions where entropy spontaneously decreases. Most of them will he small, but one day there'll come a large fluctuation, one in which particles form, say, a sugar molecule just coincidentally. Wait some more, and you'll get an entire cell. Wait even more, and eventually a fully functional brain will pop out of the high-entropy soup for long enough to think, "Here I am," and then disappear again, washed away by entropy increase. Why does it disappear again? Because that's the most likely thing to happen.

These self-aware, low entropy fluctuations are Boltzmann brains, after Ludwig Boltzmann, who in the late nineteenth century developed the notion of entropy we now use in physics. That was before the advent of quantum mechanics, and Boltzmann was concerned with purely statistical fluctuations in collections of particles. But quantum fluctuations add to the problem. With quantum fluctuations, pleiotropy objects (brains!) can appear even out of vacuum and then they disappear again.

You might think that brains fluctuating into existence is pushing things a little too far. You wouldn’t be alone. The physicist Seth Lloyd said about Boltzmann brains, "I believe they fail the Monty Python test: Stop that! That's too silly!" Or, as Lee Smolin once put it to me, “Why brains? Why isn't anyone ever talking about livers fluctuating into existence?" Fair point. But I side with Sean Carroll; I think that Boltzmann brains have something worthwhile to teach us about cosmology,

The issue with Boltzmann brains isn't so much the brains themselves; it's that the possibility of such large fluctuations leads to predictions that disagree with our observations. Remember that the lower the entropy, the less likely the fluctuation. Entropy has tube small enough to explain the observations you have made so far. Atte very least, that would be your brain with all the input you have gotten in your life. But then the theory predicts with overwhelming probability that the next thing you will see is that plant Earth disappears and entropy relaxes back to equilibrium. Well, that obviously didn't happen. It didn't happen again just now. Still hasn't happened. Meanwhile, you have thoroughly falsified the prediction.

Certainly it isn't good if a theory leads to predictions that disagree with observations. Something must be wrong, but what? The short comings in our understanding of entropy that I named earlier (gravity, continuous fields) still apply, but there is another assumption in the Boltzmann brain argument that's more likely to be the culprit. It’s that not all types of evolution laws give rise to all possible fluctuations.

A theory in which any kind of fluctuation will eventually happens called an ergodic theory. The little batter-mixing model we used is ergodic, and the models that Boltzmann and his contemporaries studied are also ergodic. Alas, it is an open question whether the theories we currently use in the foundations of physics are ergodic.

One hundred fifty years ago, physicists were concerned with par-tickles that bump into one another and change direction, and asked questions like "How long does it take until all oxygen atoms collect intone corner of the room?" That's a good question (answer: a very, very long time; don't worry), but to talk about the creation of something as complex as a brain, you need to get particles to stick together. They must form bound states, as physicists say. Protons, for example, a rebound states of three quarks, held together by the strong nuclear force. Stars are also bound states; they are gravitationally bound. Just bouncing particles off one another isn't enough to create a universe that resembles the one we actually observe. And no one yet knows whether gravity and the strong nuclear force are ergodic, so there is no contradiction in the Boltzmann brain argument.

Indeed, we can instead read the argument backward and conclude that at least one of our fundamental theories can't be ergodic. That’s why I think Boltzmann rains are interesting-they tell us something about the properties that the laws of nature must have. But you don’t need to worry that you're a lonely brain in empty space. If you were, you’d almost certainly just have disappeared. Or if you haven't already, then you'll disappear now, Or now ...

Boltzmann brains are a theoretical device to lead an argument by contradiction (if the laws of nature were ergodic, then your observations would be incredibly unlikely], but you almost certainly aren’t one. However, there is, I think, a deeper message in the paper trail that Boltzmann brains left in the scientific literature.

The foundations of physics give us a closer look at reality, but the closer we look at reality, the more slippery it becomes. Our heavy use of mathematics is a major reason. The more the fundamental descriptions of nature have become divorced from our everyday experience, the more we must rely on mathematical rigor. This reliance has consequences. Using math to describe reality means that the same observations can be equivalently explained in many different ways. That’s just because there are many sets of mathematical axioms that will give the exact same predictions for all available data. Thus, If you want to assign 'reality" to one of your explanations, you won't know which.

For example, in Isaac Newton's day, arguing that the gravitational force is real would have been uncontroversial. It was an enormously useful mathematical tool to calculate anything from the path of a For example, in Isaac Newton's day, arguing that the gravitational force is real would have been uncontroversial. It was an enormously useful mathematical tool to calculate anything from the

path of a cannonball to the orbit of the moon. But along came Albert Einstein, who taught us that the effect we call gravity is caused by the curvature of space-time; it's not a force. Does this mean the gravitational force stopped existing with Einstein? That would mean that what is real depends on what humans believe to be real Most scientists wouldn't want to go there.

Well, you may say, it's not that the gravitational force stopped existing with Einstein. It never existed in the first place. Pre-Einstein scientists were just wrong! Ah, but in that case, you can't claim that anything in our current theories is real, for one day these theories might be replaced by better ones. Space? Electrons? Blackholes? Electromagnetic radiation? You would not be allowed to call these real. Again, most scientists would balk at such a notion of reality

Even leaving aside this problem of impending paradigm shifts, it's ambiguous what mathematics you use to describe observations, because in physics we have dual theories. Two theories that are dual describe the same observable phenomena in entirely different mathematical form. Dual theories are like the drawing that, depending on what way you look at it, is either a rabbit or a duck (figure 6). Is it really a rabbit or really a duck? Well, really, it's just a dark line on a white background that you can interpret one way or the other.

In physics, the most famous example is the gauge-gravity duality. It’s a mathematical equivalence that links a higher-dimensional gravitational theory (one with curved space-time) to a particle theory intone dimension less without gravity (e.g., in flat space-time). In both theories you have a prescription to calculate measurable quantities [like, say, the conductivity of a metal). These mathematical elements of the theories (of gravity or partials) are different, and the prescriptions to calculate with them are different, but the predictions inexactly the same.

Now, it's somewhat controversial whether the gauge-gravity duality actually describes something we observe in our universe. Lots of string theorists believe it does. I, too, think there's a fair chance incorrectly describes certain types of plasma that are dual to particular types of black holes. (Or are they black holes dual to some kind of plasma?) But whether this particular dual theory correctly describes nature is somewhat beside the point here. The mere possibility of dual theories supports the conclusion drawn from the threat of im-pending paradigm changes: we can't assign "reality" to any particular formulation of a theory. (The various different interpretations of quantum mechanics are another case in point, but please allow me to postpone this discussion to chapter 5.)

It is because of headaches like this that philosophers have put for-ward a variant of realism called structural realism. Structural realism has it that what's real is the mathematical structure of a theory, not any particular formulation of it. It's the rabbit duck shape of the drawing, if you wish. Einstein's theory of general relativity structurally contains what was previously called the gravitational forefemurs we can derive this force in an approximation called the Newtonian Hit. Just because that limit isn't always a good description for our observations fit breaks down near the speed of light and when space-time is strongly curved) doesn't mean it's not real.

In structural realism, you can call gravitational forces real even though they're only approximations. You are also allowed to all spice-time real, even though it might one day be replaced with something more fundamental a big network, maybe? Because whatever the better theory is, it will have to reproduce the structure we currently use in suitable limits. It all makes sense.

If I were a realist, I'd be a structural realist. But I am not. The reason is that I can't rule out the possibility that I'm a brain in a vat and that all my supposed knowledge about the laws of nature is an elaborate illusion. I may be able to reason myself to conclude it's implausible I'm a fluctuation in an otherwise featureless universe, given all I have learned in my life, but that still doesn't prove there is any universe he sides my brain to begin with. Solipsism may be called a philosophy, but it's born out of biological fact. We are alone in our heads, and, at least so far, we have no possibility to directly infer the existence of anything besides our own thoughts.

Even so, while I contend that I can never be entirely sure anything besides myself exists, I also find it a rather useless philosophy to dwell on. Maybe you don't exist, and it's just my illusion that I've written this book, but if I can't tell an illusion from reality, why bother trying? Reality certainly is a good explanation that comes in handy. For all practical purposes, therefore, I'll deal with my observations as if they were real, granting the possibility in case someone asks-that I am not perfectly sure citer this book or its readers actually exist.

>> THE BRIEF ANSWER

We get older because that's the most likely thing to happen. Our current theories are described well by the one directional nature of time and our perception of Now. Some physicists consider the existing explanations unsatisfactory, and it is certainly worth looking for better explanations, but we have no reason to think this is necessary, of even possible. If you want to believe you're a brain in a vat, that's all right, but I wonder what difference you think it makes.