Chapter 8

DOES THE UNIVERSE THINK?

Size Matters

According to the most recent observations from the Hubble Space Telescope, our universe contains at least 200 billion galaxies. These galaxies are not uniformly distributed under the pull of gravity, they lump into clusters, and the clusters form superclusters. Between these clusters of different sizes, galaxies align along thin threads, the galactic filaments, which can be several hundred million lightyears long. Galactic clusters and filaments are surrounded by voids that contain very little matter. Altogether, the cosmic web looks somewhat like a human brain (figure 13).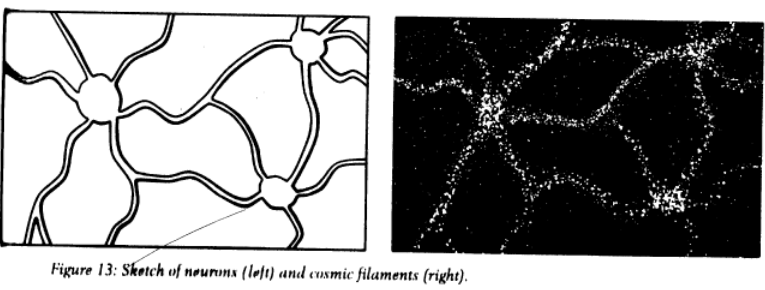

            To be more precise, the distribution of matter in the universe looks a little like the connectome, the network of nerve connections in the human brain. Neurons in the human brain, too, form clusters, and they connect by axons, long nerve fibers that send electrochemical impulses from one neuron to another.

The resemblance between the human brain and the universe is not entirely superficial; it was rigorously analyzed in a 2020 study by the Italian researchers Franco Vazza (an astrophysicist) and Alberto Feletti (a neuroscientist). They calculated how many structures of different sizes are in the connectome and in the cosmic web, and reported “a remarkable similarity." Brain samples on scales below about 1 millimeter and the distribution of matter in the universe up to about 300million lightyears, they find, are structurally similar. They also point out that, "strikingly," about three fourths of the brain is water, which is comparable to the three fourths of the universe's matter energy budget that's dark energy. In both cases, the authors note, these three fourths are mostly inert.

Could it be, then, that the universe is a giant brain in which our galaxy is merely one neuron? Maybe we are witnessing its self-reflection while we pursue our own thoughts. Unfortunately, this idea flies in the face of physics. Even so, it's worth looking at, because understanding why the universe can't think teaches an interesting lesson about the laws of nature. It also tells us what it would take for the universe to think.

In a nutshell, the universe can't think, because it's too big. Remember that Einstein taught us there is no absolute rest, so we can speak of the velocity of one object only relative to another. This is not the case for sizes. It's not only relative sizes that matter. It's absolute sizes that determine what an object can do.

Take, for example, an atom and a solar system. At first sight, the two have a lot in common. In an atom, the negatively charged electrons are attracted to the positively charged nucleus by the electric force. The strength of this force approximately falls with the familiar 1/R2law, where R is the distance between the electron and the nucleus. Ina solar system, a planet is attracted to its sun by the gravitational force. Strictly speaking, that'd be described by general relativity, but a sun’s gravity can be well approximated by Newton's 1/R2 law, where R is the distance between the planet and the sun. Atoms and solar systems are really quite similar in this regard. Indeed, this is how many physicists thought about atoms at the beginning of the twentieth century; it’s basically how the 1913 Rutherford Bohr model works.

But we know today that atoms aren't little solar systems (figure 14). Electrons aren't small balls that orbit around the nucleus; they have pronounced quantum properties and must be described by wave functions. An electron's position is highly uncertain within the atom, and its probability distribution is a diffuse cloud that takes on symmetrical shapes, called orbitals. The electrons' energy in the orbitals comes indiscrete steps it is quantized. This quantization gives rise to the regularities we find in the periodic table.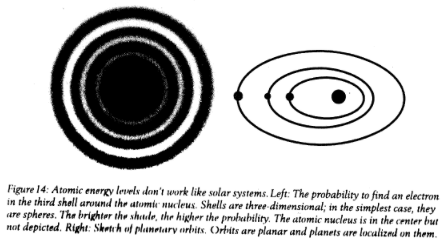            This doesn't happen for solar systems. Planets in solar systems can be at any distance from the sun. They aren't fluffy probability distributions, the orbits aren't quantized, and there's no periodic table of solar systems. Where does this difference come from?

The major reason solar systems are different from atoms is that atoms are smaller and their constituents lighter. Because of quantum mechanics, everything small particle but also a large object Hasan intrinsic uncertainty, an irreducible blurriness in position. The typical quantum blurriness of an electron (its Compton wavelength) is about 2 x 1012 meters. It's similar to the size of a hydrogen atom, which is about 5 x 1011 meters. That these sizes are comparable is why quantum effects play a big role in atoms. But if you look at the typical quantum uncertainty of planet Earth, that's about 1066 meters and entirely negligible compared with our planet's distance from the Sun, which is about 150 million kilometers (93 million miles). The physical properties size and mass make a real difference. Scaling up anatomy does not give us a solar system. That's just not how nature works. To use the technical term, the laws are not scaling invariant.

Why aren't the laws of nature scale invariant? It's because of those twenty-six constants. They determine which physical processes are important on which scales, and each scale is different. We see this scale dependence of physics come through in biology. For small animals like insects, friction forces (created by contact interactions) are much more important than for large animals, like us. That’s why ants can crawl up walls and birds can fly, whereas we can’t. We're just too heavy. A human size, human weight ant would be an evolutionary disaster and still couldn't crawl up walls. It's not the shape that allows small animals to master these feats; it's just that they don't have to fight so much against gravity.

Let us, then, look at how similar the universe actually is to a brain, keeping in mind that those constants of nature make a difference. The universe expands, and its expansion is speeding up. How fast the expansion speeds up is determined by the cosmological constant, which is the simplest type of dark energy. Brains, in contrast, don’t normally expand, unless possibly metaphorically, and they also don’t expand along with the universe: the brain is held together by electromagnetic and nuclear forces, which are much stronger than the pull that the cosmological expansion exerts. Even galaxies themselves are held together by their own gravitational pull and don't expand together with the universe. It's only somewhere between the distances of galaxy clusters and filaments that the expansion of the universe wins over and stretches the galactic web.

So if galaxy clusters were the universe's neurons, then they'd be flying apart from one another with ever-increasing relative speedometer have been doing so for some billion years already. Dark energy maybe "inert," as Vazza and Feletti wrote in their paper, but it plays an important role for the structure of the universe. And while the fraction of dark energy in the universe is similar to the fraction of water in the brain, water doesn't expand the brain. (Or if it does, that's bad news.)

The other constant that makes a major difference between the universe and the brain is the speed of light. Neurons in the human brain send about 5 to 50 signals per second. Most of these signals (80 percent) are short distance, going only about 1 millimeter, but about 20 percentage long-distance, connecting different parts of the brain. We need both to think. The signals in our brain travel at 100 meters per second (225miles per hour), a million times slower than the speed of light. Before you conclude that's really slow, let me add that pain signals travel even slower, at only about 1 meter per second. I recently bumped my toe on the door while I happened to be looking at my foot. I just about managed to think, "It's going to hurt," before the pain signal actually arrived. Maybe our universe is smarter than Einstein and has figured out a way to signal faster than light. But let's put aside such speculations for now and stick with established physics. The universe is now some 90billion lightyears in diameter. This means if one side of the hypothetical universe brain wanted to take note of its other side, that "thought “would take 90 billion years at least to arrive. Sending a single signal tour nearest galaxy cluster/neuron (the M81 Group) would take about11 million years, even at the speed of light. At most, the universe might have managed about a thousand exchanges between its nearest neurons in its lifetime so far. If we leave the long-range connections entirely aside, that's about as much as our brain does in three minutes. And the capacity of the universe to connect with itself decreases with its expansion, so it'll go downhill from now on.

The bottom line is, if the universe is thinking, it isn't thinking very much. The amount of thinking that the universe could conceivably have done since it came into existence is limited by its enormous size and size matters. The physics just doesn't work out. If you want to do a lot of thinking, it helps to keep things small and compact. There’s still the question whether the whole universe might be connected in a way we don't yet understand, a way that allows it to overcome the speed flight limit and do some substantial thinking. Such connections are often attributed to entanglement in quantum mechanics, a nonlocal quantum link that can span large distances. Particles that are entangled share a measurable property, but we don’t know which particle has which share until we measure it. Suppose you have a big particle whose energy you know. It decays into two smaller particles: one flies left; one flies right. You know that the total energy must be conserved, but you don't know which of the decay products has which share they are entangled: the information about the total energy is distributed between them. According to quantum mechanics, which of the small particles has which share of the total energy will be determined only when you make a measurement. But once you measure the energy share of one of the small particles, that of the other small particle which meanwhile could bear away is also determined, immediately.

That indeed sounds like something you might use to signal faster than light. However, no information can be sent with this measurement, because the outcome is random. The experimenter who measures one of the particles cannot ensure he will get a particular outcome, so he has no mechanism by which to impress information onto the other particle.

The idea that entanglement is an instantaneous connection over long distances is fertile ground for science myths. Two years ago, I took part in a panel discussion together with another author, who'd recently published a book about dinosaurs. ª Just because, I suppose, the paleontology section is next to physics. The host, in his best attempt to transition from dinosaurs to quantum mechanics, asked me whether the dinosaurs might have been entangled throughout the universe with the meteoroid that spelled their doom.

That transition deserves a prize, but if you look at the physics, the idea makes no sense. First, as we discussed earlier, quantum effects get washed out incredibly quickly for big objects like you and me, dinosaurs, and meteoroids. Really, you can debunk 99 percent of quantum pseudoscience just by keeping in mind that quantum effects are incredibly fragile. You can't cure diseases with quantum entanglement any more than you can build houses from air, and you can't use entanglement to explain the demise of the dinosaurs either. Maybe more important, entanglement in quantum mechanics is often portrayed as much more mysterious than it really is. While entanglement is indeed nonlocal, it is still created locally. If I break apart a cookie and give you one half, then these two halves are nonlocally correlated because their lines of breakage fit together even though they’re spatially separated. Entanglement is a nonlocal correlation like that, but it's quantitatively stronger than the cookie correlation. I don't want to downplay the relevance of entanglement. That quantum correlations are different from their nonquantum counterparts is why quantum computers can do some calculations faster than conventional computers. But the reason for this computational advantage is not that the quantum correlations are nonlocal; it's that entangled particles can do several things at the same time (with the warning that that's a verbal description of mathematics that has no good verbal description).

I believe the major reason so many people think entanglement is what makes quantum mechanics "strange" is that it's almost always introduced together with the Einstein quote "spooky action at a distance." Einstein indeed used this phrase (or its German translation, “spectate Firewalking") to refer to quantum mechanics. But he didn’t use it to refer to entanglement. He was referring instead to the reduction of the wave function. And that is indeed nonlocal if you think it, is a physical process.

Now, most physicists today don't think the reduction of the wavefunction is physical, but we don't know for sure what is going on. Aspen rose pointed out, it's a gap in our understanding of nature. And this is only one of the reasons physicists in the past decades have toyed with the idea of bona fide nonlocality, not just nonlocal entanglement, but actual nonlocal connections in spacetime through which information can be sent across large distances instantaneously, faster than the speed of light.

This isn't necessarily in conflict with Einstein's theories. Einstein’s special and general relativity don't forbid faster than light motion per se. Rather, they forbid accelerating something from below to above the speed of light, because that would take infinite energy. The speed of light is thus a barrier, not a limit. Neither does faster than light motion or signaling necessarily lead to causality paradoxes the type where someone travels back in time, kills their own grandfather, and is never born and so they can't travel back in time. Such causality paradoxes can occur in special relativity when faster than light travel is possible, because an object that moves faster than light for one observer can look as if it's going back in time for another observer. Thus, in special relativity, you always get both together: faster than light motion and backward Intime motion, and that opens the door to causality paradoxes.

In general relativity, however, causality problems can't occur, because the universe expands and that fixes one direction of time as forward. This forward Intime direction is related to the forward Intime direction from entropy increase. The exact relation between them is still somewhat unclear, but that's not so relevant here. What’s relevant is only that the universe arguably has a forward direction intime. For this reason, nonlocality and faster than light signaling are neither in conflict with Einstein's principles nor necessarily unphysical.

Instead, if they existed, that might solve some problems in the current theories for example, the issue that information seems to get lost in black holes, which creates an inconsistency with quantum mechanics (see chapter 2). A black hole horizon traps light and everything slower than light, but nonlocal connections can cross the horizon. With them, information can escape and the problem is solved. Some physicists have also suggested that dark matter is really a misattribution. There may be only normal matter whose gravitational attraction is multiplied and spread out because of nonlocal connections in spacetime.

These are speculative ideas without empirical support, and I can’t say I am enthusiastic about them. I mention them just to demonstrate that nonlocal connections spanning the universe have been seriously considered by physicists. They're farfetched, all right, but not obviously wrong.

Where might such nonlocal connections come from? One possibility is that they were left behind from gametogenesis. As we briefly discussed in chapter 2, gametogenesis is the idea that the universe is fundamentally a network that merely approximates the smooth space of Einstein's theories. However, when the geometry of spacetime was created from the network in the early universe, defects might have been left in it. This means, as Photini Markopoulos and Lee Smolin pointed out in 2007, space would today be sprinkled with nonlocal connections (figure 15).

            You can think of those nonlocal connections as tiny wormholes, shortcuts that connect two normally distant places. These nonlocal connections would be too small for us, or even elementary particles, Togo through. They'd have a diameter of merely 1035 meters. But they would tightly connect the geometry of the universe with itself. And there’d be loads of these connections. Markopoulos and Smolin estimate our universe would contain about 10360 of them. The human brain, for comparison, has a measly 1015. And because these connections are nonlocal anyway, it doesn't matter that they expand with space. I have no particular reason to think these nonlocal connections actually exist, or that, if they existed, they'd indeed allow the universe to think. But I can't rule this possibility out either. Crazy as it sounds, the idea that the universe is intelligent is compatible with all we know so far.

Is There a Universe in Each Particle?

In the previous section, we saw that the laws of nature are not scale free; that is, physical processes change with the size of objects. But there is a weaker form of scale freeness that you may be familiar with: fractals. Take, for example, the Koch snowflake. It's generated by adding smaller equilateral triangles to equilateral triangles, as shown in figure 16a. The shape you get if you continue adding triangles indefinitely is a fractal; the area is finite, but the length of the perimeter is infinite.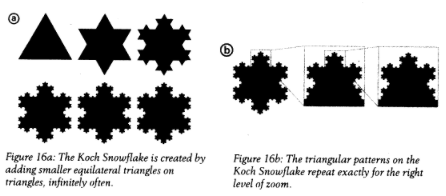

The Koch snowflake is not scale free; it changes if you zoom in none of its corners. But at the right levels of zoom, the pattern will repeat exactly (figure 16b). If you keep on zooming, it will repeat again and again. We say the Koch snowflake has discrete scale variance’s pattern repeats only for certain values of the zoom, not all of them. If our universe is not scale free, then can it have discrete scale invariance instead, so each particle harbors a whole universe? Maybe there are literally universes inside us. The mathematician and entrepreneur Stephen Wolfram has speculated about this: "[Maybe] down at the Planck scale we'd find a whole civilization that's setting things up so our universe works the way it does."

For this to work, structures wouldn't need to repeat exactly during the zoom. The smaller universes could be made of different elementary particles or have somewhat different constants of nature. Evenson, the idea is difficult to make compatible with what we already know about particle physics and quantum mechanics.

To begin with, if the known elementary particles contain Mini universes that can come in many different configurations, then why do we observe only twenty-five different elementary particles? Why aren’t there billions of them? Worse, simply conjecturing that the known particles are made up of smaller particles or are made up of galaxies containing stars containing particles, etc. doesn't work. The reason is that the masses of the constituent particles (or galaxies or whatever) must be smaller than the mass of the composite particle because masses are positive and they add up. This means the new particles must have small masses.

But the smaller the mass of a particle, the easier it is to produce in particle accelerators. That's because to produce the particle, the energy in the particle collision has to reach the energy equivalent of the particle’s mass (E = mc2!). Particles of small mass are thus usually the first to be discovered. Indeed, if you look at the order in which elementary particles were discovered historically, you'll see that the heavier ones came later. This means if each elementary particle were made up of smaller things, we'd long ago have seen them.

One way to get around this problem is to make the new particles strongly bound to one another, so it takes a lot of energy to break the bonds even though the particles themselves have small masses. Thesis how it works for the strong nuclear force, which holds quarks together inside protons. The quarks have small masses but are still difficult to see, because you need a lot of energy to tear them apart from one another.

We don't have evidence that any of the known elementary particles are made up of such strongly bound smaller particles. Physicists have certainly thought about it, though. Such strongly bound particles that could make up quarks are called prions. But the models that have been proposed for this run into conflict with data obtained by the Large Hadron Collider, and by now most physicists have given upon the idea. Some sophisticated models are still viable, but in any case, with such strongly bound particles, you cannot create something that resembles our universe. To get structures similar to what we observe, you'd need an interplay of both long-distance forces (like gravity) and short distance forces (like the strong nuclear force). Another way the Mini universes might be compatible with observation would be if the particles they're made up of interacted only very weakly with the particles we know already: they'd just pass through normal matter. In that case, producing them in particle colliders could also be unlikely, and they might hence have escaped detection. This is why the elementary particles called neutrinos, even though they have small masses, were discovered later than some of the heavier particles. Neutrinos interact so rarely that most of them go through detectors instead of leaving a signal. However, if you want to make a Mini universe from such weakly interacting, low mass particles, this creates another problem. They should have been produced in large amounts in the early phase of our universe (as, indeed, neutrinos were), and we should have found evidence for that. Alas, we haven't.

As you see, it isn't easy to come up with ways to build the known elementary particles from something else other particles or microscopic galaxies without running into conflict with observations. Thesis because the standard model of particle physics has kept up for so long.

There is another problem with the idea of putting new particles inside the already known ones, and that is Heisenberg's uncertainty relation. In quantum mechanics, the less mass a particle has, the more difficult it is to keep the particle confined in small regions of space, like inside another elementary particle. If you try to make a Mini universe by stuffing a lot of new, low mass particles into a known elementary particle, they'll just escape by quantum tunneling.

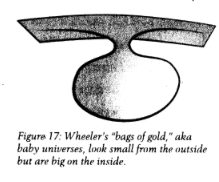
You can circumvent this problem by conjecturing that the inside of our elementary particles has a large volume. Like the TARDIS in Doctor Who, they might be bigger on the inside than they look from the outside. Sounds crazy, I know, but it's indeed possible. That's because in general relativity we can curve spacetime so strongly that it'll form bags (figure 17). These bags can have a small surface aerie., look small from the outside but have a large volume inside. The physicist John Wheeler (who introduced the terms black hole and wormhole) called them "bags of gold." (It was one of his less catchy phrases.)

The problem is, they are unstable the opening will close off, giving rise to either a black hole or a disconnected baby universe. We'll talk about those baby universes in the next interview, but because they don’t stay in our space, they can't be elementary particles. And if elementary particles were black holes, they'd evaporate and also disappear pretty much immediately. Not only is this something we've never seen elementary particles doing, but it's also a process that'd violate conservation laws we know to be valid. Or, if you'd managed to find a way to prevent evaporation, they could merge to larger black holes, which is incompatible with the observed behavior of elementary particles.

Maybe there's a way to overcome all these problems, but I don’t know one. I therefore conclude that the idea that there are universes inside particles is incompatible with what we currently know about the laws of nature.

Are Electrons Conscious?

It's time to talk about panpsychism. That's the idea that all matter animates or inanimate is conscious; we just happen to be somewhat more conscious than carrots. According to panpsychism, consciousness is everywhere, even in the smallest elementary particles. This idea has been promoted, for example, by the alternative medicine advocate Deepak Chopra, the philosopher Philip Goff, and the neuroscientist Christof Koch. As you can tell already from this list of names, it's a mixed bag. I'll do my best to sort it out.

First let us note that in the entire history of the universe, not a single thought has been thought without having come about through physical processes; hence, we have no reason to think consciousness (or anything else, for that matter) is nonphysical. We don't yet know exactly how to define consciousness, or exactly which brain functions are necessary for it, but it's a property we observe exclusively in physical systems. Because, well, we observe only physical systems. If you think your own thoughts are an exception to this, try thinking without your brain. Good luck.

Panpsychism has been touted as a solution to the problem of dualism, which treats mind and matter as two entirely separate things. Asi mentioned earlier, dualism isn't wrong, but if mind is separate from matter, it has no effect on the reality we perceive; hence, it's clearly antiscientific idea. Panpsychism aims to overcome this problem by declaring consciousness fundamental, a property that is carried by any kind of matter it’s everywhere.

In panpsychism, every particle carries preconsciousness and has rudimentary experiences. Under some circumstances, like in your brain, the preconsciousness’s combine to give proper consciousness. You will see immediately why physicists have a problem with this idea. The fundamental properties of matter are our terrain. If there were a way to add or change anything about them, we’d know.

I realize that physicists have a reputation of being narrowminded. But the reason we have this reputation is that we tried the crazy stuff long ago, and if we don't use it today, it's because we've understood that it doesn't work. Some call it narrowmindedness; we call it science. We have moved on. Can elementary particles think? No, they can’t. It's in conflict with evidence. Here's why.

The particles in the standard model are classified by their properties, which are collectively called quantum numbers. The electron, for example, has an electric charge of 1, and it can have a spin value of+1/2 or 1/2. There are a few other quantum numbers with complicated names, such as the weak hypercharge, but exactly what they're called is not so important. What's important is that there are a handful of those quantum numbers and they uniquely identify the types of elementary particles.

If you then calculate how many new particles of certain types are produced in a particle collision, the result depends on how many variants of the produced particle exist. In particular, it depends on the different values the quantum numbers can take. That's because this is quantum mechanics, and so anything that can happen will happen. If a particle exists in many variants, you'll therefore produce them all, regardless of whether or not you can distinguish them.

Now, if you want electrons to have any kinds of experiences however rudimentary they might be then they must have multiple different internal states. But if that were so, we'd long ago have seen it, because it would change how many of these particles are created in collisions. We didn't see it; hence, electrons don't think, and neither do any other elementary particles. It's incompatible with data.

There are some creative ways you can try to wiggle out of this conclusion, and I've suffered through them all. Some panpsychists try to argue that to have experiences, you don't need different internal states; preconsciousness is just featureless stuff. But then claiming that particles have "experiences" is meaningless. I might as well claim that eggs have karma, just that you can't see karma and it has no properties either.

Next you can try to argue that maybe we don't see the different internal states in elementary particles, and they become relevant only in large collections of particles. That doesn't solve the problem, though, because now you'll have to explain how this combination happens. How do you combine featureless preconsciousness to something that suddenly has features? Philosophers call it the combination problem of panpsychism, and, yeah, it's a problem. In fact, if preconsciousness is physically featureless, it's exactly the same problem as trying to understand how elementary particles combine to create conscious systems.

Finally (and this is what my discussions on the topic usually come down to), you can just postulate that preconsciousness doesn’t have any measurable properties, and its only observable consequences that it can combine to what we normally call consciousness. And that’s fine in the sense that it doesn't conflict with evidence. But now you just have a weird version of dualism in which unobservable conscious stuff is splattered all over the place. It's by construction both useless and unnecessary to explain what we observe; hence, it’s scientific again.

In brief, if you want consciousness to be physical "stuff," then you’ll have to explain how its physics works. You can't have your cake and eat it too.

Now that I've told you why panpsychism is wrong, let me explain why it’s right.

The most reasonable explanation of consciousness, it seems to me, is that it's related to the way some systems like brains process information. We don't know exactly how to define this process, but this almost certainly means that consciousness isn't binary. It's not an on off, either-or property, but gradual. Some systems are more conscious, others less, because some process more information, others less.

We don't normally think about consciousness that way because, for everyday use, a binary classification is good enough. It's like how, for most purposes, separating materials into conductors and insulators is good enough, though, strictly speaking, no material is perfectly insulating.

There has to be a minimum size for systems to be conscious, however, because you need to have something to process information with. An object that is indivisible and internally featureless like electronica’s do that. Just exactly where the cutoff is, I don't know. I don't think anyone knows. But there has to be one, because the properties of elementary particles have been measured very accurately already and they don't think we've just discussed.

This notion of panpsychism is different from the previously discussed one because it does not require altering the foundations of physics. Instead, consciousness is weakly emergent from the known constituents of matter; the challenge is to identify under exactly which circumstances. That's the real "combination problem."

There are various approaches to such physics compatible panpsychism, though not all advocates are equally excited about adopting the name. The aforementioned Christof Koch is among those who have embraced the label panpsychist. Koch is one of the researchers who support integrated information theory, IIT for short, which is currently the most popular mathematical approach to consciousness. Itas put forward by the neurologist Giulio Tomoni in 2004.

In IIT, each system is assigned a number, ¢ (Greek capital phi), which is the integrated information and supposedly a measure of consciousness. The better a system is at distributing information while it’s processing the information, the larger the phi. A system that’s fragmented and has many parts that calculate in isolation may process lots of information, but this information is not integrated, so phi is small.

For example, a digital camera has millions of light receptors. It processes large amounts of information. But the parts of the system don’t work much together, so phi is small. The human brain, on the other hand, is very well connected and neural impulses constantly travel from one part to another, so phi is large. At least that's the idea. But IIT has its problems.

One problem with IIT is that computing phi is ridiculously time-consuming. The calculation requires that you divide up the system you’re evaluating in every possible way and then calculate the connections between the parts. This takes an enormous amount of computing power. Estimates show that even for the brain of a worm with only three hundred synapses, calculating phi with state-of-the-art computers would take several billion years. This is why measurements of phi that have actually been done in the human brain used incredibly simplified definitions of integrated information for example, by calculating connections merely between a few big parts, not between all possible parts.

Do these simplified definitions at least correlate with consciousness? Well, some studies have claimed they do. Then again, others have claimed they don't. The magazine New Scientist interviewed Daniel Boor from the University of Cambridge and reported, "Phi should decrease when you go to sleep or are sedated via a general anesthetic, for instance, but work in Boor’s lab has shown that it doesn’t. ‘It either goes up or stays the same,' he says."

Yet another problem for IIT, which the computer scientist Scott Aaronson has called attention to, is that one can think of rather trivial systems that solve some mathematical problem but that distribute information during the calculation in such a way that phi becomes very large. This demonstrates that phi in general says nothing about consciousness.

There are some other measures for consciousness that have been proposed: for example, the amount of correlation between activity indifferent parts of the brain, or the ability of the brain to generate models of itself and of the external world. Personally, I am highly skeptical that any measure consisting of a single number will ever adequately represent something as complex as human consciousness, but this isn't so relevant here. What's relevant is that we can scientifically evaluate how well measures of consciousness work.

I have to add some words about Mary's room, because people still bring it up to me in the attempt to prove that perception isn't a physical phenomenon. Mary's room is a thought experiment put forward by the philosopher Frank Jackson in 1982. He imagines that Mary isa scientist who grows up in a black-and-white room, where she studies the perception of color. She knows everything there is to know about the physical phenomenon of color and the brain's reaction to color. Jackson asks, "What will happen when Mary is released from her black-and-white room or is given a color television monitor? Will she learn anything or not?"

He goes on to argue that Mary learns something new upon perceiving color herself, and that therefore the sensation of color is not the same as the brain state of the perception. Instead, the mind has a nonphysical aspect the qualia.

The flaw in this argument is that it confuses knowledge about the perception of color with the actual perception of color. Just because you understand what the brain does in response to certain stimuli (color perception or other), it doesn't mean your brain has that response. Jackson himself later abandoned his own argument.

Fact is, scientists can today measure what goes on in the human brain when people are conscious or unconscious, can create experiences by directly stimulating the brain, can literally read thoughts, and have taken first steps to develop brainstorming interfaces. There is so far zero evidence that anything about human perception is nonphysical.

I don't find that surprising. The idea that consciousness can't be scientifically studied because it's a subjective experience never made sense, because one's own subjective experience is all any scientist has ever had to work with. They might have believed it's objective, all right, but in the end, it was all inside their head. And that will remain unless, mayhem, we one day solve the solipsism problem by actually connecting brains.

The advice of philosophers of science is certainly still needed in consciousness research to sort out what properties a satisfactory definition of consciousness must fulfill, what questions it can answer, and what counts as an answer. But the study of consciousness has left the realm of philosophy. It is now science.

>> THE BRIEF ANSWER

Going by the currently established laws of nature, the universe can’t think. However, physicists are considering that the universe has many nonlocal connections because that could solve several problems in the existing theories. It's a speculative hypothesis, but if it's correct, the universe might have enough rapid communication channels to be conscious. However, the idea that there are universes inside particles and that particles are conscious are both either in conflict with evidence or scientific. Because consciousness quite possibly isn't a binary variable, some versions of panpsychism are compatible with physics.