Chapter 9

ARE HUMANS PREDICTABLE?

The Limits of Math

Do you remember the scene from Basic Instinct? No, not that one. I mean the scene where they walk up the stairs and he say, "I'm very unpredictable," but she says "unpredictable" along with him. We’re not remotely as unpredictable as we like to think.

Indeed, many aspects of human behavior are fairly easy to predict. Reflexes, for example, short-circuit conscious control for the sake of speed. If you hear a sudden, loud sound, I can predict you'll twitch and your heart rate will spike. Other aspects of human behavior are predictable for group averages; they stem, among other things, from the constraints of economic reality, social norms, laws, and upbringings. Take the unsurprising fact that traffic is usually worse during rush hour. Indeed, mobility patterns are in general 93 percent predictable, according to an analysis of data collected from mobile phone users. I can also predict that in North America, undressing in public will bring you a lot of attention. And that Brits drink tea, watch cricket, and if you have a foreign accent, will inevitably explain to you that the Queen owns the swans in England. A

Stereotypes are amusing exactly because humans are, to some extent, predictable. But is human behavior entirely predictable? It is arguably not currently entirely predictable, but that's the boring answer. Is it possible in principle, given all we know about the laws of nature? If you are a compatibilist who believes your will is free because your decisions can't be predicted, must you fear that you will become predictable one day?

In 1965, the philosopher Michael Scriven argued that the answers no. Scriven claimed there is an "essential unpredictability in human behavior" using what is now called the paradox of predictability. It goes like this: Suppose you are given the task of making a decision. For example, I offer you a marshmallow, and you either take it or not. Now let us imagine I predicted your decision and told you about it. Then you could do the opposite, and my prediction would be false! Hence, human behavior has an unpredictable element. It's important that Scriven's argument works even if human behavior is entirely determined by, say, the initial state of the universe. Predictability, it seems, does not follow from determinism.

This conclusion is correct, but it has nothing to do with human behavior in particular. To see why, suppose I write a computer code whose only task is to output YES or NO to the question whether an input number is even. Then I add a clause saying that when the input further contains the correct answer to the first question, the output is the negation of the first answer. That is, the input "44" would resulting YES, but the input "44, YES" would result in NO. By Scriven's argument, there'd be something essentially unpredictable about that computer code too.

Indeed there is, because the prediction for the code's output depends on the input; it's unpredictable without it. There are lots of systems that have this property; for example, your being offered the marshmallow: Your reaction depends on what I say when I offer it. But that doesn't mean it was fundamentally unpredictable; it just means it wasn't predictable from insufficient data. If you'd put the two of us into a perfectly isolated room, then, in a deterministic world, you could predict what both of us would do, and also whether you’d take the marshmallow.

So Scriven's argument doesn't work. But if you've been paying attention, then you know that human behavior is partly unpredictable just because quantum mechanics is fundamentally random. It is somewhat unclear just what role quantum effects play in the human brain, but you don't need those. You could just use a quantum mechanical device or maybe pull up that Universe Splitter app on orphaned decide whether or not to take the marshmallow. And I couldn’t predict that decision. I could still, however, predict the probability of your making a particular decision, and I could test how good my predictions are byrunning the experiment repeatedly, the same way we test quantum mechanics. So, really, when we are asking whether human behavior is predictable, we should be asking more precisely whether the probabilities of decisions are predictable. Insofar as the current laws of nature are concerned, they are and to the extent they aren't predictable, they aren't under your control.

However, this conclusion seems to be contradicted by some results from computer science. In computer science, there are certain types of problems that are undecidable, meaning it's been mathematically proven that no possible algorithm can solve the problem. Could not something similar go on in the human brain?

One of the best-known undecidable problems is the domino problem, posed by Hao Wang in 1961. Assume you have a set of square tiles. Draw an X on each of them, so you get four triangles on each tile. Then fill each triangle with a color (figure 18). Can you cover an infinite plane with those tiles so the colors of adjacent tiles all fit together if you're not allowed to rotate the tiles or leave gaps? That’s the domino problem. It is easy to see that, for certain sets of tiles, the answer is yes, it is possible. But the question Wang posed is: If I give you an arbitrary set of tiles, can you tell me whether it'll tile the plane?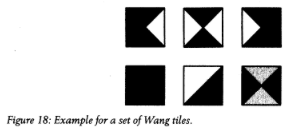

This problem, it turns out, is undecidable. One can't write computer code that'll answer the question for all sets of tiles. This was proved in 1966 by Robert Berger, who showed that Wang's domino problem is a variant of Alan Turing's halting problem. The halting problem poses the question whether an input algorithm will finish running at a finite time or continue calculating forever. The problem, Turing showed, is that there is no meta-algorithm that can decide whether any given input algorithm will or won't halt. Likewise, there is no meta-algorithm that can decide whether any given set of tiles will or won't tile the plane.

However, the undecidability of both the domino problem and the halting problem comes from the requirement that the algorithm answer the question for a system of infinite size. In the domino problem, that's all-possible sets of tiles; in the halting problem, it's all possible input algorithms. There are infinitely many of both of them. We already saw this earlier, in chapter 6, when we discussed the question whether some emergent properties of composite systems are incomputable. These incomputable properties occur only if some quantity becomes infinitely large, which never happens in reality certainly not in the human brain.

So if we can't argue that our decisions might be algorithmically undecidable, what about the argument from Gödel's incompleteness theorem that Roger Penrose brought up? Penrose's argument isn’t about predictability, but about computability, which is a somewhat weaker statement. A process is computable if it can be produced by a computer algorithm. The current laws of nature are computable, except for that random element from quantum mechanics. If they were incomputable, though, that'd make space for something new, maybe even unpredictability.

Let us use the approach to Gödel's theorem that Penrose mentioned, which he credits to Stour ton Steen. We start with a finite setoff axiom and imagine a computer algorithm that generates theorems derived from those axioms, one after another. Then, Gödel showed, there is always a statement, formulated within this system of axioms, that is true but that the algorithm cannot prove to be true. This statement is usually called the Gödel sentence of the system. * It's constructed so it implicitly states that it's unprovable within the system. Therefore, the Gödel sentence is true exactly because it can't be proven, but its truth can be seen only from outside the system. It might seem, then, that because we can see the truth of the Gödel sentence, whereas the algorithm can't, there's something about human cognition that a computer doesn't have. However, this particular insight about the Gödel sentence is incomputable only by that particular algorithm. And the reason we can see the truth of this Foresentence is that we have more information about the system than does the algorithm that's creating all those theorems we know how the algorithm itself was programmed.

If we gave that information to a new algorithm, then the new algorithm would see the truth of the previous algorithm's Gödel sentence, just as we do. But then we could construct another Gödel sentence for the new algorithm, and another algorithm that recognizes the new Gödel sentence, and so on. Penrose's argument is thus that, because we can see the truth of any Gödel sentence, we can do more than any conceivable algorithm.

The problem with this argument is that computer algorithms, suitably programmed, are for all we can tells capable of abstract reasoning as we are. We can't count to infinity any better than a computer, but we can analyze the properties of infinite systems, both countable and uncountable ones. So can algorithms. That way, Gödel’s theorem itself has been proven algorithmically. Hence, some algorithms, too, can "see the truth" of all Gödel sentences.

There are a number of other objections that have been raised to Penrose’s claim, but most of them likewise come down to pointing out that humans simply wouldn't see the truth of a Gödel sentence without further information like Gödel's theorem either. However, I do find quite charming the argument that humans would recognize V x Puffs (x," GF 7) as obviously true. That's an idea only a mathematician could come up with.

Could a computer have come up with the proof of Gödel’s theorem on its own? That's an open question. But at least for now, Penrose’s argument doesn't show that human thought is noncompatible far, we haven't found any loophole that would allow human behavior to be unpredictable. But what about chaos? Chaos is deterministic, but just because it's deterministic doesn't mean it can be predicted. Indeed, chaos could be more of a problem for predictability than commonly thought, because of what Tim Palmer dubbed the "real butterfly effect."

The common butterfly effect has it that the time evolution of a chaotic system is exquisitely sensitive to the initial conditions; the smallest errors (a butterfly flap in China) can make a large difference later (a tornado in Texas). The real butterfly effect, in contrast, means that even arbitrarily precise initial data allow predictions for only a finite amount of time. A system with this behavior would be deterministic and yet unpredictable.

However, while mathematicians have identified some differential equations with this behavior, it is still unclear whether the real butterfly effect ever occurs in nature. Quantum theories are not chaotic to begin with and therefore can't suffer from the real butterfly effect. In general relativity, singularities can prevent us from making predictions beyond a finite amount of time, like inside black holes or at the Big Bang. However, as we discussed earlier, these singularities likely just signal that the theory breaks down and needs to be replaced with something better. And if general relativity is one day completed by a quantum theory, then that, too, cannot have a real butterfly effect. The best chance for a breakdown of predictability comes like the “common" butterfly effect from weather forecasts. In this case, the dynamical law is the Navier Stokes equation, which describes the behavior of gases and fluids. Whether the Navier Stokes equation always has predictable solutions is still unknown. Indeed, it is number four on the list of the Clay Mathematics Institute's Millennium Problems.

But the Navier Stokes equation is not fundamental; it emerges from the behavior of the particles that make up the gas or fluid. And we already know that fundamentally on the deepest levelheaded are described by quantum theories again, so their behavior is predictable, at least in principle. This does not answer the question whether the Navier Stokes equation always has predictable solutions, but if it doesn't, it's because the equation does not take into account quantum effects.

So far it seems we have no reason to think human behavior incomputable, that human decisions are algorithmically undecidable, or that human behavior might be predictable for only a finite amount of time. Especially in light of the neuron replacement argument from chapter 4, it full well looks as though we can simulate brains on a computer and therefore predict human behavior.

Physics puts several obstacles in the way, however. Perhaps the most important one is that replacing a neuron is not the same as copying aneurin. If we wanted to predict a human's behavior, we'd first have to produce a faithful model of the person's brain. For that, we'd have to measure its properties somehow and then copy that information into our prediction machine, whatever that might be. However, in quantum mechanics, the state of a system cannot be perfectly copied without destroying the original system. This no cloning theorem makes it provably impossible for people to know exactly what is going on inside your brain, because if they knew, they'd have changed your brain. Therefore, if any relevant details of your thoughts are in quantum format, they are "unknowable" and hence unpredictable.

Quantum effects, however, might not actually matter very much to exactly define the state of your brain. Even if they don't, though, there’s another obstacle in the way of predicting human behavior. Our brains are not particularly good at crunching through difficult math problems, but they're remarkably efficient for making complex decisions while running on only about 20 watts, about the power consumption of a laptop. If you could produce a simulation of a human brain on a computer, it's therefore questionable that it would actually run faster than the brain it's trying to simulate. To use the term coined by Stephen Wolfram, human deliberation might be computable but not computationally reducible, and therefore not predictable, in the sense that the calculation may be correct, but too slow.

It's not an implausible conjecture that part of our behavior is computationally irreducible. The human brain was optimized by natural selection over hundreds of thousands of years. If someone wanted to predict it, they'd first have to build a machine capable of doing the same thing, faster. However, for the same reason that it's been produced by natural selection it’s also unlikely that the human brain is really the fastest way to compute what our brains compute. Natural selection isn't in the business of coming up with the best overall solutions. Solutions just have to be good enough to survive. And if we take into account that a computer would not be required to be as energy efficient as the brain, I suspect it'll be possible to outdo the human brain in speed. But it'll be difficult.

For the same reason, I strongly doubt we will ever derive morals, as Sam Harris has argued, from whatever knowledge we gather about the human brain. Even if it does become possible, it'd just be too time consuming. It is much easier to just ask people what they think, which is, in a nutshell, what our political, economic, and financial systems do. Or at least what they should do.

In summary: we have no reason to think human behavior is unpredictable in principle, but good reason to think it's very difficult to predict in practice.

AI Fragility

Having discussed the challenges in the way of simulating human behavior, let us talk for a bit about attempts to create artificial general intelligence. In contrast to the artificially intelligent systems we use right now, which specialize in certain tasks like recognizing speech, classifying images, playing chess, or filtering shaman artificial general intelligence would be able to understand and learn as well as humans, or even better.

Many prominent people have expressed worries about the aim to develop such a powerful artificial intelligence (AI). Elon Musk thinks it’s the "biggest existential threat." Stephen Hawking said it could "bathe worst event in the history of our civilization." Apple cofounder Steve Wozniak believes that AIs will "get rid of the slow humans Torun companies more efficiently." And Bill Gates, too, put himself in “the camp that is concerned about super intelligence." In 2015, the Future of Life Institute formulated an open letter calling for caution and formulating a list of research priorities. It was signed by more than eight thousand people.

Such worries are not unfounded. Artificial intelligence, like any new technology, brings risks. While we are far from creating machines even remotely as intelligent as humans, it's only smart to think about how to handle them sooner rather than later. However, I think these worries neglect the more immediate problems AI will bring.

Artificially intelligent machines won't get rid of humans anytime soon, because they'll need us for quite some while. The human brain may not be the best thinking apparatus, but it has distinct advantages over all machines we have built so far: It functions for decades. It’s robust. It repairs itself. Some million years of evolution optimized not only our brains but. Also our bodies, and while the result could certainly be further improved (damn those knees), it's still more durable than any silicon-based thinking apparatuses we have created to date. Some AI researchers have even argued that a body of some kind is necessary to reach human level intelligence, which if correct would vastly increase the problem of AI fragility.

Whenever I bring up this issue with AI enthusiasts, they tell me that AIs will learn to repair themselves, and even if they don't, they will just upload themselves to another platform. Indeed, much of the perceived AI threat comes from their presumed ability to replicate themselves quickly and easily, while at the same time being basically immortal. I think that's not how it will go.

It seems more plausible to me that artificial intelligences at first will be few and one of a kind, and that's how it will remain for a longtime. It will take large groups of people and many years to build and train artificial general intelligences. Copying them will not be any easier than copying a human brain. They'll be difficult to fix once broken, because, as with the human brain, we won't be able to separate the hardware from the software. The early ones will die quickly for reasons we will not even comprehend.

We see the beginning of this trend already. Your computer isn’t like my computer. Even if you have the same model, even if you run the same software, they're not the same. Hackers exploit these differences between computers to track your internet activity. Canvas fingerprinting, for example, is a method of asking your computer to render a font and output an image. The exact way your computer performs this task depends on both your hardware and your software; hence, the output can be used to identify a device.

At present, you do not notice these subtle differences between computers all that much (except possibly when you spend hours browsing help forums, murmuring, "Someone must have had this problem before," but turn up nothing). The more complex computers get, the more obvious the differences will become. One day, they will be individuals with irreproducible quirks and bugs like you and me. So we have AI fragility plus the trend that increasingly complex hard and software becomes unique. Now extrapolate this some decades into the future. We will have a few large companies, governments, and maybe some billionaires who will be able to afford their own AI. Those AIs will be delicate and need constant attention from crew of dedicated humans.

If you think about it this way, a few problems spring up immediately:

1. Who gets to ask questions, and what questions? This may not be a matter of discussion for privately owned AIs, but what about those produced by scientists or bought by governments? Does everyone get a right to a question per month? Do difficult questions have to be approved by the parliament? Who ‘sin charge?

2. How do you know you are dealing with an AL? The moment you start relying on AIs, there's a risk that humans will use them to push an agenda by passing off their own opinions as those of the AI. This problem will occur well before Als are intelligent enough to develop their own goals. Suppose a government uses AI to find the best contractor for a lucrative construction task. Are you sure it's a coincidence that the biggest shareholder of the chosen company is the brother of a high-ranking government official?

3. How can you tell if an AI is any good at giving answers? If you have only a few Als, and those are trained for entirely different purposes, it may not be possible to reproduce any of their results. So how do you know you can trust them? It could be a good idea to require that all AIs have a common area of expertise that can be used to compare their performance.

4. How do you prevent the greater inequality, both within nations and between nations, inevitably produced by limited access to AL? Having an AI to answer difficult questions can be a great advantage, but left to market forces alone, it's likely to make the rich richer and leave the poor even further behind. If this is not something that the "unrich" want and I certainly, don’t we should think about how to deal with it.

Personally, I have little doubt that an artificial general intelligence is possible. It may become a great benefit for human civilizational great problem. It is certainly important to think about what ethics to code in to such intelligent machines. But the most immediate problems we will have with Als will come from our ethics, not theirs.

Predicting Unpredictability

I've spent most of this book discussing what physics teaches us about our own existence. I hope you've enjoyed the tour, but maybe you sometimes couldn't avoid the impression that this is heady stuff that doesn’t do much to solve problems in the real world. And so, as we near the end of this book, I want to spend a few pages on the practical consequences that understanding unpredictability may have in the future.

Let us return to the problem of weather forecasting. We are not going to solve the fourth Millenium Problem here, so for the sake of the argument, let us just assume that solutions to the Navier Stokes equation are indeed sometimes unpredictable beyond a finite time. As I've explained, we already know that the Navier Stokes equation isn’t fundamental; it instead emerges from quantum theories that describe all particles. But, fundamental or not, understanding the properties of the Navier Stokes equation tells us what we can reasonably hope to achieve by solving it.

If we knew we couldn't improve weather forecasts, because a mathematical theorem said it was impossible, we might, for example, conclude it doesn't make sense to invest huge amounts of money into additional weather measurement stations. Whether the Navier Stokes equation is fundamentally the right equation doesn't make this investment advice any less sound; it matters only that it's the equation meteorologists use in practice.'

This is an oversimplified case, of course. In reality, the feasibility of a prediction depends on the initial state: some weather trends are easy to predict over long periods, others not. But again, understanding what can be predicted in the first place isn't just idle mathematical speculation. It's necessary to know what we can improve, and how. Let us pursue this thought a little further. Suppose we got really good at doing the weather forecast, so good that we could figure out exactly when the Navier Stokes equation is about to run into an unpredictable situation. This could then allow us to find out which small interventions in the weather system could change the weather to our liking.

Scientists have indeed considered such weather control, for example, to prevent tropical cyclones from growing into hurricanes. They understand the formation of hurricanes well enough to have come up with methods for interrupting their growth. At present, the major problem is that the weather predictions just aren't good enough to figure out exactly when and where to intervene. But preventing hurricanes, or controlling the weather in other ways, isn't a hopelessly futuristic idea. If computing power continues to increase, we might actually be able to do this within a few decades.

Chaos control also plays a role in many other systems for example, the plasma in a nuclear fusion plant. This plasma is a soup of atomic nuclei and their disconnected electrons with a temperature of more than 100 million degrees Celsius (180 million degrees Fahrenheit). It sometimes develops instabilities that can greatly damage the containment vessel. If an instability is coming on, therefore, the fusion process must be rapidly interrupted. This is one of the main reasons it is so difficult to run a fusion reactor energy efficiently.

However, plasma instability is in principle avoidable if we can predict when an unpredictable situation is about to come up, and if we can control the plasma so the situation is averted. In other words, if we understand when a solution to the equations becomes unpredictable, we can use that knowledge to prevent it from happening in the first place.

This is not just the fantasy of a theorist; a recent study looked into exactly this. A group of researchers trained an artificially intelligent system to recognize data patterns that signal an impending plasma instability. They were able to do this with good success, using only data in the public record. A second ahead, they correctly identified an imminent instability in somewhat more than 80 percent of cases; 30milliseconds ahead, they saw almost all instabilities coming. Granted, theirs was a hindsight analysis, with no option of active control. However, should we become good enough making such predictions, active control might become possible in the future. An energy efficient fusion plant, in the end, might be a matter of finetuning with advanced machine learning.

A similar consideration applies for a superficially entirely different system that, however, has many parallels to plasma blowups and weather forecasts: the stock market. Today, a whole army of financial analysts makes money by trying to predict the selling and buying of stocks and financial instruments, a task that now includes predicting their competitors' predictions. But every once in a while, even they get caught by surprise. A stock market crashes, vendors panic, everyone blames everyone else, and the world slumps into a recession.

But imagine we could tell in advance when trouble is at the front door; we might be able to close the door.

It's not only unpredictability that we might want to recognize in order to avoid it, but also computability. Take the economic system. It is a self-organized, adaptive system with the task of optimizing the distribution of resources. Some economists have argued that this optimization is partly incomputable. That's clearly not good, fort means the economic system cannot do its job. Or rather, we as agents in the economic system cannot do our job, because trading does not have the desired result.

Creating an economic system that can actually do the desired optimization (in finite time) has motivated the research line of computable economics. And as with unpredictability, what makes impossibility theorems relevant for computable economics is not proving that the solution to a problem (here: how to best distribute resources) is fundamentally incomputable may or may not be but merely that itis incomputable with the means we currently have.

In other situations, however, unpredictability is something we may want to trigger rather than avoid, for the same reason that randomness can sometimes be beneficial; for example, to prevent computer algorithms that search for optimal solutions from getting stuck. Think of the computer algorithm as a device that, when you dump it into a mountainous landscape, will always move uphill. The landscape stands for the possible solutions to a problem and the height foursome quantity you want to optimize, say, the accuracy of a prediction. In the end, the computer algorithm will sit on a hill the local

optimum but what you actually wanted to find was the highest hill the global optimum (see figure 19). Adding stochastic noise can prevent this from happening, because the algorithm then has a chance to coincidentally discover a better solution. Counterintuitively, therefore, an element of randomness can improve the performance of mathematical code.

global optimum

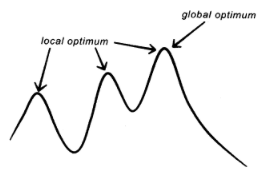local optimum Figure 19: Local vs. global optimum.

In a computer algorithm, randomness can be implemented by a(pseudo) random number generator without drawing on complicated mathematical theorems. But unpredictability might well be useful for optimization in other circumstances. For example, small doses could aid the efficiency of the economic system. Even more interesting, unpredictability might be an essential element of creativity, and thus something that artificial intelligence could draw on in the future.

Already, right now, artificial intelligence is better at discovering patterns in large sets of data than we are. This is about to change science dramatically. Human scientists look for universal scattershot are robust under changes in the environment and easy to infer. That’s how most science has proceeded so far. By using artificial intelligence, we can now look for patterns that are much more difficult to discern. The development of personalized medicine is one consequence, and we will almost certainly see more of this soon. Instead of looking for universal laws, scientists will increasingly be able to track exact dependencies on external parameters in ecology and biology, for example, but also in social science and psychology. There is vast discovery potential here.

Physicists should take note too. The universal laws they have found might only scratch the surface of sofa unrecognized complexity. While my colleagues think they are closing in on a final answer, I think we’ve only just begun to understand the question.

>> THE BRIEF ANSWER

Human behavior is partially predictable, but it's questionable that it’ll ever be fully predictable. At the very least, it's going to be extremely difficult and won't happen any time soon. Instead of worrying about simulating human brains, we should pay more attention to who gets to ask questions of artificial brains. Understanding the limits of predictability isn't merely of mathematical interest but is also relevant for real-world applications.