Chapter 5
DO COPIES OF US EXIST?
Many Worlds
Popular-science news about quantum mechanics is to me as baffling as it is frustrating. Hand me an equation, and I can deal with it. But if you tell me that quantum mechanics allows one to separate a cat from its grin or that an experiment shows "an irreconcilable mismatch, be-tween the friends and the Wigner’s," I'll back out of the room quietly before anyone demands I explain this mess. I have suffered through countless well-intended introductions to quantum mechanics featuring quantum shoes, quantum coins, quantum boxes, and entire zoos of quantum animals that went in and out of those boxes. If you act-ally understand those explanations, I salute you, because if I hadn’t known already how quantum mechanics works, I still wouldn't know.
I am telling you this not to undermine your fun with quantum shoes, but so you understand where I am coming from. I am very much a math person, and personally I don't see the need to translate math into everyday language. Abstract mathematical structures, I think, are best dealt with on their own terms. They don't need to be interpreted, and they don't need to make intuitive sense. They don’t have to be "like" anything else-because in most cases, they are not. The whole reason we use this math is that there isn't anything else like it.
To me, quantum mechanics is the prime example for what can go wrong with using intuitive language for abstract math. Take super-positions. In quantum mechanics, we put initial states into the Schrödinger equation to calculate how they change in time. The Schrödinger equation has the property that if we have solved it for two different initial states, then the sum of those solutions, each multiplied by arbitrary numbers, is also a solution to the equation. ª And that's what a superposition is: A sum. That's it. No, I'm not joking. Entangled states are a specific type of superposition. Yes, they're also sums. So where did all the fabled weirdness go?
The weirdness appears only if you try to express the math verbally. If one of the states that solved the Schrödinger equation describes a particle moving to the right, and the other one a particle moving to the left, then what's the sum of those? It has become common to use the phrase "the particle goes in both directions at the same time. “Does that adequately describe what a superposition is? In all honesty, I don't know. I'd prefer to leave it at "it's a superposition."
Of course, I understand the need to express mathematics in words to make it accessible, which is why I myself have used metaphors for superpositions when I don't have time or space to explain the details. And I will do the same here: omit the math and try to give you an idea of what it all means. But I want you to know that much of the supposed weirdness of quantum mechanics just comes from forcing it into everyday language. There are no exact metaphors, not for quantum mechanics and not for anything else, because if they were exact, they wouldn’t be metaphors.
It doesn't help that calling quantum mechanics strange, weird, or spooky makes for catchy headlines, and thus popular-science outlets use these words a little too frequently and a little too gleefully. I agree with Philip Ball that, at more than a hundred years of age, quantum mechanics should move "beyond weird." Having said that, let us look at what quantum mechanics tells us about afterlife.
Without quantum mechanics, the laws of nature are deterministic. To recap, this means if you have an initial state, you can calculate unambiguously what happens at any later time. Say you drop a pen and it falls to the ground. If you could measure exactly where and from which position the pen started, and if you knew the exact locations and motions of all the air, molecules around it, you could calcium-late when and how the pen would land.
Of course, we can't measure the positions of all air molecules ex-aptly, and even if we could, using them to predict the outcome would be unfeasible. But in principle, without quantum mechanics, any un-certainty about the outcome arises merely from our lack of know-edge about the initial conditions. We call these types of nonquantum theories classical.
Quantum mechanics works differently. In quantum mechanics, we describe everything by wave functions. There is a wave function for electrons and one for photons, but there are also wave functions for grapefruits, brains, and even one for the whole universe. These wave functions evolve partly deterministically, but every once in a while, when a measurement takes place, they make indeterministic jumps.
These jumps are not entirely unpredictable-we can predict the probability that they happen and the probability for their outcome-but they have an element that is fundamentally random. This uncertainty in the outcome of a measurement in quantum mechanics is not due to our lack of knowledge about the initial conditions; according to quantum mechanics, that's just how it is.
This unpredictable randomness of quantum mechanics is not con-fined to subatomic scales, so it's not like you can just wave it away as an irrelevant quirk of nature that scientists occasionally see in their laboratories. Exactly because the outcome of a measurement is what’s unpredictable, the randomness manifests itself for macroscopic ob.-jects like you and me.
Suppose that an experimenter observing a flash on a screen goes home when the particle appears on the left side and stays in the lab when it appears on the right side. Maybe that decides whether or not she gets into an accident on the highway. The randomness of a single quantum event can change her whole life. And this doesn't happen only in the laboratory. If a cosmic ray hits living tissue, the damage to the genetic code, for example, ultimately comes down to quantum indeterminism.
But while quantum mechanics is an extremely successful theory, just what its mathematics means has been disputed since the develop-mint of the theory at the beginning of the twentieth century. Some have argued that nature can't be fundamentally random-like Ein-stein, who claimed that "God does not play dice"-and that quantum mechanics is just incomplete. Others, like one of the founders of quantum mechanics, Niels Bohr, have claimed that we just need to get over old-fashioned ideas of determinism.
Most physicists today ignore the entire debate and deal with Quan-tum mechanics as a tool that makes predictions and that one shouldn’t overthink. This "shut up and calculate" attitude is the pragmatic way to go about it. It has led to great progress, so it shouldn't be laughed off. However, many researchers who work in the foundations of physics feel that ignoring the problems of quantum mechanics is a mistake because we'd learn more from resolving them.
To understand the problem with quantum mechanics, recall that in Einstein's theory of special relativity, nothing can happen faster than the speed of light. Yet in quantum mechanics, the moment you make a measurement, probabilities change, instantaneously and every-were. This update of the wave function is nonlocal. It is, as Einstein put it, a "spooky action at a distance." Alas, it turns out that in that process of measurement, no information is submitted faster than the speed of light. Indeed, one can mathematically prove it's impossible to send information faster than the speed of light with quantum me-chances. So it's not as though there's something concretely wrong with the theory. It just feels wrong.
Researchers have proposed various ways to deal with this situation. Some argue that quantum mechanics is just not the right theory and has to be replaced with something better. This is a possibility I have worked on myself, but because it's both speculative and some-what off topic, I don't want to go into this here. For the purposes of this book, I will stick with what is widely considered the accepted status of research.
If you don't want to actually change quantum mechanics, you can try to interpret the mathematics differently and hope that then it makes more sense. There are a number of such interpretations. For example, there’s the interpretation proposed by Niels Bohr, according to which the wave function just shouldn't be considered real. It's a device to make predictions for measurements, Bohr said, but if you are not making a measurement, it is meaningless to ask what is really happening. This is now often called the Copenhagen interpretation or just the stan-Dard interpretation, because it's the most commonly taught one.
Needless to say, a lot of physicists don't like being told they're not supposed to ask questions, so they have tried to find other, more in-fugitive ways to make sense of the math. One alternative interpretation was pursued by David Bohm, and is known today as Bohmianmechanics.
Bohm reformulated the equations of quantum mechanics so they look more similar to those of classical mechanics. In Bohm's equations, the wave function is still there, but now it describes a field that “guides" particles. The indeterminism in the measurement outcomes, according to Bohm's interpretation, is due to a lack of knowledge, as it is in classical physics. Alas, Bohemian mechanics also has it that you can never remedy that lack of knowledge. In the end, the outcome is exactly the same as in the Copenhagen interpretation. Bohm's inter-predation never became very popular, but it still has its followers today.
Yet another way of interpreting quantum math was pioneered by. Hugh Everett and further developed by Bryce DeWitt. They argued that one should just get rid of the measurement update and thereby return to a deterministic evolution. In the many-worlds interpretation, each possible measurement outcome happens, but it happens in its own universe. If you think back to the particle that had a fifty-fifty chance of hitting the screen on the left side or the right side, then in the many-worlds interpretation, it will hit the screen on the right side in one universe and on the left side in another universe. And after it does that, these two universes will remain separated forever-they will evolve in their own branches, as they are often called.
Before we can move on, I have to sort out a common mis under-standing with the many-worlds interpretation. One way to explain how quantum mechanics works, one you may have come across, is that particle takes every possible path from its initial to its final place. For example, if one points a laser beam at a screen with two slits (the famous double slit), then each particle in the laser beam goes through both slits. It's not that one particle goes through the left and the next one through the right slit; each goes through both slits (figure 8).
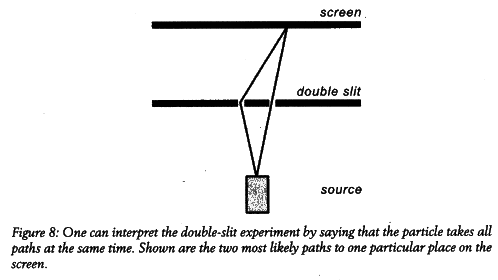
This, again, is an interpretation of the mathematics, originally pro-posed by Feynman, called the path-integral approach. Mathematically, you then have to sum over all the possible paths to calculate the prob-ability of the particle to go to one particular place. To make a long story short, the result is the same as in the original formulation with the Schrödinger equation, but physicists like using path integrals be-cause the approach can be generalized to more-difficult situations.
One can interpret the path integral as telling us that the particle takes each path in a different universe. Personally, I find this a rather meaningless statement-there isn't anything in the math that says these paths are in different universes-but it isn't wrong either. Andi am all for different ways of looking at math because they can lead to new insights. So, OK.
However, these different paths-or universes, if you wish-in the usual path integral are present only before the measurement. Ianthe many-worlds interpretation, in contrast, the different universes still exist after the measurement. So just because we can reformulate quantum mechanics in terms of a path integral doesn't mean the many-worlds interpretation is correct. These are two different things.
The key feature of the many-worlds interpretation is that each time a quantum measurement happens, the universe splits, creating what’s commonly called a multiverse. ª And because we've seen earlier that (with some apologies about the abuse of terminology) even inter-actions with air or the cosmic microwave background can cause a measurement, that creates a lot of universes really quickly. It also makes a lot of physicists uncomfortable really quickly.
The problem with the idea is that, well, no one's ever seen a unit-verse splitting. According to the many-worlds interpretation, that’s because detectors and their generalization-like you and I-split to-gather with the universes. What determines which universe you go into? Ah, you supposedly go into all of them. Because that isn't what we experience, the many-worlds interpretation requires further as-Sumption’s (besides the Schrodinger equation) that specify how to calculate the probability of going into one particular universe. This brings indeterminism in again through the back door.
I'll spare you the mathematical details because they don't really matter. The upshot is that you need to add sufficiently many assumptions to reproduce the predictions of what was formerly called the measurement update. Because-you know what? - it was there for a reason, the reason being that it's necessary to describe what we observe, and if you just throw it away, then the theory simply does not give the right predictions. We do not, as a matter of fact, observe all possible outcomes of an experiment.
This means that as far as calculations are concerned, the many-worlds interpretation makes exactly the same predictions as quantum. Mechanics in the standard interpretation, from equivalent, yet differ-entry expressed, assumptions. The major difference isn't in the math; the major difference is one of belief. Advocates of the many-worlds interpretation believe that all the other universes-the ones we don’t observe-are as real as ours.
But in which sense are they real? Unobservable universes are by definition unnecessary to describe what we observe. Hence, assuming they are real is also unnecessary. Scientific theories should not contain unnecessary assumptions, for if we allow that, we would also have to allow the assumption that a god made the universe. Such superfluous assumptions aren't wrong. They're just a scientific. The assumption that the additional universes in the many-worlds interpretation are real is one such a scientific assumption.
I must stress that this doesn't mean that the parallel universes of the many-worlds idea are not real. It means that any statement about their reality is a scientific. It is something you can believe or disbelieve, but science tells you nothing-can tell you nothing-about what is correct. Conversely, this also means that the idea that there are infinitely many you out there, somewhere, doesn't conflict with anything we know. It's a science-compatible belief system.
It does have a few odd consequences, though. For example, because deep down all our brain processes are quantum processes, for every decision you make, there'll be a universe in which you chose the other option. And just in case you aren't sure a decision was indeed based on quantum effect, there's an app for this: the Universe Splitter sends a photon through a semitransparent mirror for you, and depending on whether it goes through or not, you can choose either pasta or chicken, accept or decline, take the red pill or the blue, all the while believing that a copy of your lives out the option you didn't choose.
That's quite something already, but the best example of odd multiverse consequences may be the idea of quantum suicide. Imagine you repeat an experiment in which a quantum process kills you with 50percent probability. In the standard interpretation of quantum me-chances, the probability of your survival goes down by half in each repetition of the experiment. By the twentieth repetition, the probability that you are dead is 99.9999 percent.
However, according to the many-worlds interpretation, you don’t die with 50 percent probability in each round. Instead, the first time you run the experiment, the universe splits into two universes, one in which you die and one in which you survive. In the second run, each of the two universes splits, so you have four. In two of them you died already in the first round, so the second experiment doesn't matter. Then there's one in which you survived the first round but die in the second, and one in which you survive both. Do the experiment again and all four universes split to make eight, and so on (see figure 9). After twenty rounds, you are still alive with 100 percent probability, but only in one of a million universes.
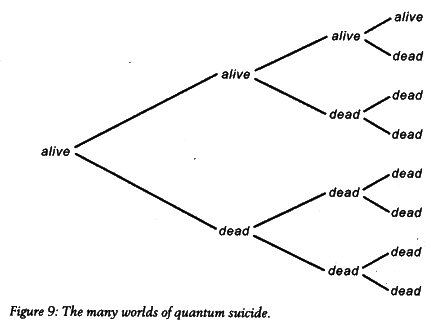
It gets better. Because every molecular process comes down to quantum mechanics, this means that whatever the cause of some-body's death, that person had a tiny, yet nonzero, probability of survival-quantum randomness makes it possible. There is always the chance that an illness will spontaneously go into remission, that cell damage will suddenly revert, or that a heart will start beating again after having given up. And even if the chance of that happening is minuscule, in the many-worlds interpretation, it will happen-for every one of us-in some branch of the multiverse.
This, of course, also means there's a branch in the multiverse in which dinosaurs still roam the world, Hitler was never born, and spray cheese was never invented. That's arguably not the branch we live in, so what are we to make of all that?
If you believe in the many-worlds interpretation, reasoning about probabilities in our universe becomes reasoning about numbers of branches in the multiverse. And because you can't go back intime to choose a different branch, those probabilities are relative to your present observation of the universe. For all practical per-poses, the outcome is exactly the same: dinosaurs are extinct, the Second World War happened, and spray cheese is a thing. You may not die in all branches of the multiverse, but the probability of your survival (or that of the dinosaurs) decreases just the same as it does in the standard interpretation. That's why no one's attempted Quan-tum suicide: it would decrease the number of universes in which they survive.
As far as observations are concerned, the many-worlds inter-predation doesn't make any difference. But if you like to believe there are infinitely many copies of you living all possible alternative versions of your life, go ahead. That belief isn't in conflict with science.
The Multiwire
The many-worlds interpretation is only one type of multiverse. There are a few others that have become popular in past decades.
One is an extension of the idea of inflation, the hypothetical phase of exponential expansion in the early universe. In this extension, eternal inflation, one invents a mechanism to create the initial state for inflation in our universe. The currently most popular way of doing this is to conjecture a multiverse in which Big Bangs happen all the time and everywhere. The universes created in the other Big Bangs could be similar to our own, or they could have different constants of nature, leading to entirely different physical laws.
That the constants of nature might change from one Big Bang to another comes from another multiverse idea: the string-theory land-scape. String theorists originally hoped they'd be able to calculate the constants of nature. That didn't pan out, so now they argue that if they can't calculate the constants, that must mean all possible values exist somewhere in a multiverse.
You can combine all these different multiverses to one megamouth-verse.
As in the many-worlds interpretation, in the other multiverses, the universes besides our own are also by construction unobservable. And they are inhabited by even more copies of you, but these copies come about for a different reason: small variations in the initial state can lead to universes with histories almost, but not exactly, like the history of our own universe. Of course we don't actually know, and will never know, what initial states are actually possible in the multiverse because we can't gather observational evidence for them. This is pure conjecture.
The scientific status of these multiverse ideas is thus the same as that of the many-worlds interpretation. Assuming the reality of some-thing unobservable is unnecessary to describe what we observe. Hence, assuming that these other universes are real is a scientific.
This isn't a particularly difficult argument, so I find it stunning that my physics colleagues can't seem to comprehend it. Inevitably, they will declare, "But then one would also have to argue that talking about the inside of black holes isn't scientific." But, no, the situation for black holes is entirely different. For one, you can (in principle!) totally observe what's inside a black hole. You just can't come back to tell us about it. More important, black holes evaporate, so their inside doesn’t eternally remain disconnected from us. When a black hole evaporates, its horizon shrinks until it's entirely gone. If that weren’t so, I would indeed question the scientific merit of talking about what’s inside a black hole.
"But," they'll argue next, "because the speed of light is finite but the universe is only 13.7 billion years old, we can merely see part of the universe, even if it's infinitely large." Yet certainly I don't believe that the universe stops existing beyond the boundary of what we can cur-gently observe.
Well, as I have explained so often, this isn't about what I believe or not; it's about what we can know or not. I am saying that what's be-yond what we can observe is purely a matter of belief. Science doesn’t say anything about whether it exists or doesn't exist. Hence, claiming it exists is a scientific, and so is claiming it doesn't exist. If you want to talk about it, fine, but don't pretend it's science. At that point, they’re usually either confused or offended or both.
The reason I keep insisting physicists clean up their act and stop conflating belief with science is that their confusion is patently obvious to non-experts. Physicists from Brian Greene to Leonard Susskind to Brian Cox to Andrei Linde have publicly spoken about the multiverse as if it were best scientific practice. And because multiverse ideas attract a lot of media attention, this sheds a bad light on the capability of the scientific community to hold its members thigh standards.
A prominent example for the damage that can result comes from2016 Republican presidential candidate Ben Carson. Carson is a re-tired neurosurgeon who doesn't seem to know much about physics, but what he knows, he must have learned from multiverse enthusiasts. On September 22, 2015, Carson gave a speech at a Baptist schooling Ohio, informing his audience that "science is not always correct. “This is, of course, correct. But then he went on to justify his science skepticism by making fun of the multiverse:
And then they go to the probability theory, and they say, "But if there’s enough big bangs over a long enough period of time, one of them will be the perfect big bang and everything will be perfectly organized."
In an earlier speech, he cheerfully added, "I mean, you want to talk about fairy tales? This is amazing."
Now, it is clear from Carson's elaborations that he has mis under-stood much of thermodynamics and cosmology, but, really, this isn’t the point. I don't expect neurosurgeons to be experts in the foundations of physics, and I hope Carson's audience doesn't expect that either. The point is, he shows us what happens when scientists mix fact with fiction: non-experts throw out both together.
In his speech, Carson went on: "I then say to them, 'Look, I'm not going to criticize you. You have a lot more faith than I have .... I give you credit for that. But I'm not going to denigrate you because of your faith, and you shouldn't denigrate me for mine.'"
And I'm with him on that. No one should be denigrated for what they believe in. If you want to believe in the existence of infinitely many universes with infinitely many copies of yourself, some of whom are immortal, that's fine with me. But please don't pretend it's science.
Do We Live in a Computer Simulation?
I quite like the idea that we live in a computer simulation. It gives me hope that things will be better on the next level. This simulation hypothesis, as it's called, has been mostly ignored by physicists, but it enjoys a certain popularity among philosophers and people who like to think of themselves as intellectual. Evidently, it's more appealing the less you understand physics.
The simulation hypothesis is most strongly associated with the philosopher Nick Bostrom, who has argued that (given certain as-Sumption’s I will come to in a moment) pure logic forces us to con-clued that we are simulated. Elon Musk is among those who have bought into it. "It's most likely we're in a simulation," he said. And even Neil deGrasse Tyson gave the simulation hypothesis "better than50-50 odds" of being correct.
The simulation hypothesis annoys me, but not because I'm afraid people will actually believe it. Most people understand that the idea lacks scientific rigor. No, the simulation hypothesis annoys me be-because it intrudes on the terrain of physicists. It's a bold claim about the laws of nature that doesn't pay any attention to what we know about the laws of nature.
Loosely speaking, the simulation hypothesis has it that everything we experience was coded by an intelligent being, and we are part of that computer code. The opinion that we live in some kind of computation in and by itself is not an outrageous claim. For all we currently know, the laws of nature are mathematical, so you could say the unit-verse is really just computing those laws. You may find this terminology a little weird, and I would agree, but it's not controversial. The controversial bit about the simulation hypothesis is that it assumes there is another level of reality where some being or something con-trolls what we believe are the laws of nature, or even interferes with those laws.
The belief in an omniscient being that can interfere with the laws of nature, but that for some reason remains hidden from us, is a com-moon element of monotheistic religions. The difference is that those who believe in the simulation hypothesis argue that they have arrived at their belief by reason. Their line of argumentation usually closely follows Nick Bostrom's argument, which, in a nutshell, goes like this: if there are (a) many civilizations, and these civilizations (b) build computers that run simulations of conscious beings, then (c) there are many more simulated conscious beings than real ones, so you are likely to live in a simulation.
First of all, it could be that one or both of the premises is wrong. Maybe there aren't any other civilizations, or they aren't interested in simulations. That wouldn't make the argument wrong, of course; it would just mean that the conclusion can't be drawn. But I will leave aside the possibility that one of the premises is wrong, because I don’t really think we have good evidence for one side or the other.
The point I have seen people criticize most frequently about Bos-Trom’s argument is that he just assumes it is possible to simulate hu-manlike consciousness. We don't actually know that this is possible. However, in this case, it would require an explanation to assume that it is not possible. That's because, for all we currently know, conscious-ness is simply a property of certain systems that process large amounts of information. It doesn't really matter exactly what physical basis this information processing is based on. It could be neurons or transistors, or it could be transistors believing they are neurons. I don’t think simulating consciousness is the problematic part.
The problematic part of Bostrom's argument is that he assumes it is possible to reproduce all our observations not using the natural laws that physicists have confirmed to extremely high precision but using a different, underlying algorithm, which the programmer is running. I don’t think that's what Bostrom meant to do, but it's what he did. He implicitly claimed it's easy to reproduce the foundations of physics with something else. This is the problematic part of the argument.
To begin with, quantum mechanics features phenomena that are not computable with a conventional computer in finite time. At the very least, therefore, one would need a quantum computer to run the simulation-that is, a computer that works with quantum bits, or-bits for short, that are superpositions of two states (say, 0 and 1).
But nobody yet knows how to reproduce general relativity and the standard model of particle physics from a computer algorithm run-Ning on any type of machine. Waving your hands and yelling "quantum computer" doesn't help. You can approximate the laws we know with computer simulation-we do this all the time-but if that were how nature actually worked, we could see the difference. Indeed, physicists have looked for signs that natural laws really proceed step by step, like a computer code, but their search has come up empty-handed. It's possible to tell the difference because all known attempts to algorithmically reproduce natural laws are incompatible with the full symmetries of Einstein's theories of special and general relativity. It’s not easy to outdo Einstein.
This problem exists regardless of what the laws are in the higher-level reality from which the programmer supposedly simulates us. We don't know any kind of algorithm that would give us the laws we observe, regardless of what that algorithm is running on. If we knew, we’d have found a theory of everything.
A second issue with Bostrom's argument is that, for it to work, a civilization needs to be able to simulate a lot of conscious beings, and these conscious beings will themselves try to simulate conscious be-Ings, and so on. While you can imagine simulating a single brain with its inputs only, in this case the conclusion we are likely to live in a simulation because there are more simulated than real brains wouldn’t work. You actually need a lot of brains. But this means you have to compress the information we think the universe contains because otherwise your simulations will run out of disk space quickly. Bos-Trom therefore has to assume it's somehow possible to not care much about the details in some parts of the world where no one is currently looking, and just fill them in in case someone looks.
Again, though, he doesn't explain how this is supposed to work. What kind of computer code can actually do that? What algorithm can identify conscious subsystems and their intention and then quickly fill in the required information without ever producing an observable inconsistency? That's a much more difficult issue than Bostrom seems to appreciate. Not only does it assume that consciousness is computationally reducible, for otherwise you couldn't predict where someone is about to look before they look, but also you can in general not just throw away physical processes on short distances and still get the long distances right.
Global climate models are an excellent example. We don't cur-gently have the computational capacity to resolve distances below something like 10 kilometers (614 miles) or so. But you can't just discard all the physics below this scale. This is a nonlinear system, so the details from short scales leave a mark on large scales-butterflies causing tornadoes and so on. If you can't compute the short-distance physics, you have to at least suitably replace it with something. Get-ting this right even approximately is a big headache. And the only reason climate scientists do get it approximately right is that they have observations they can use to check whether their approximations work. If you have only a simulation, like the programmer in the simulation hypothesis, you can't do that.
That's my issue with the simulation hypothesis. Those who believe it make big assumptions, maybe unknowingly, about what natural laws can be reproduced with computer simulations, and they don't explain how this is supposed to work. But finding alternative explanations that match all our observations to high precision is really difficult. I should know-it's what we do in the foundations of physics.
Maybe you're now rolling your eyes because, come on, let the nerds have some fun, right? And, sure, some part of this conversation is just intellectual entertainment. But I don't think popularizing the simulation hypothesis is entirely innocent fun. It's mixing science with religion, which is generally a bad idea, and, really, I think we have better things to worry about than that someone might pull the plug on us.
In summary, the simulation hypothesis isn't a serious scientific argument. This doesn't mean it's wrong, but it means you'd have to be-live it because you have faith, not because you have logic on your side.
>> THE BRIEF ANSWER
The idea that copies of us exist in the multiverse is not scientific, be-cause such copies are both unobservable and unnecessary to explain what we can observe. Multiverse theories have been promoted by physicists who believe that mathematics is real, as opposed to being a tool to describe reality. You are, therefore, welcome to believe that copies of you exist, if you want, but there is no evidence this is act-ally correct. The hypothesis that our universe is a computer simulation does not meet the current scientific standard.
| ![]()